Question

Determine the electric potential energy of a system consisting of two charges $7\mu C$ and $- 2\mu C$ (and with no external field) placed at ( $- 9cm$ , $0.0$ ) and ( $9cm$ , $0.0$ ) respectively.

Answer 1

You can start by calculating the distance between the given two charges. Then use the equation $W = \dfrac{1}{{4\pi {\varepsilon _0}}} \times \dfrac{{{q_1}{q_2}}}{r}$ to calculate the amount of work done on the system. Then explain that work done on the system is stored in the system as potential energy.

Complete answer:
In the problem, we are given a system of two charges. One charge of magnitude $7\mu C$ placed at ( $- 9cm$ , $0.0$ ), and a second charge of magnitude $- 2\mu C$ placed at ( $9cm$ , $0.0$ ).

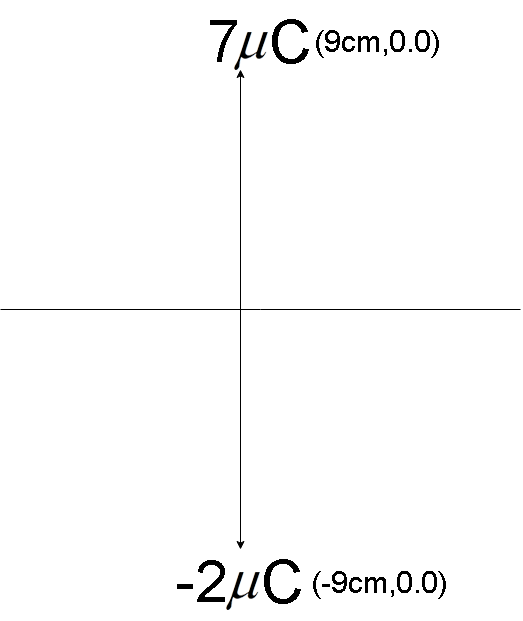
So, the distance between the two charges is $9 - \left( 9 \right) = 18cm = 18 \times {10^{ - 2}}cm$
We have to think about how the system would have been formed. Initially, both these charges would have been at an infinite distance from each other. Let’s assume that the charge of magnitude $7\mu C$ was first placed at ( $- 9cm$ , $0.0$ ). During the movement of this charge, no other charge is present. Then the charge of magnitude $- 2\mu C$ was placed at ( $9cm$ , $0.0$ ). This second charge would have moved to its respective position under the influence of electrostatic force due to the first charge, so work is done on the second charge to move it to its respective position.
We know that work done in bringing a charge from infinity to its position under the influence of another charge is given by

$W = \dfrac{1}{{4\pi {\varepsilon _0}}} \times \dfrac{{{q_1}{q_2}}}{r}$
Here, $W =$ Work done
${q_1} =$ The magnitude of one of the charges
${q_2} =$ The magnitude of the other charge
$r =$ The distance between the two charges
$W = \dfrac{1}{{4\pi {\varepsilon _0}}} \times \dfrac{{7 \times {{10}^{ - 6}} \times - 2 \times {{10}^{ - 6}}}}{{18 \times {{10}^{ - 2}}}}$
$W = - 0.7J$

This work done is stored in the system as potential energy ( $U$ ) so, $U = - 0.7J$ .

Note:
The work done in an electric field is stored in the charge as potential energy. Work is done in an electric field to move the charge against the force of attraction and repulsion applied to the charge by the electric field. This work done is only dependent on the initial and final position of the charge and the magnitude of the charge.