Question

Determine the electric field everywhere outside the sphere at a distance $r\left( { > > a} \right)$ from the centre.
(A) $E = \dfrac{Q}{{4\pi {\varepsilon _0}{r^2}}}$
(B) $E = \dfrac{Q}{{4\pi {\varepsilon _0}r}}$
(C) $E = \dfrac{Q}{{4\pi {\varepsilon _0}{a^2}}}$
(D) $E = \dfrac{Q}{{4\pi {\varepsilon _0}a}}$

Answer 1

To solve this question, we need to use the gauss theorem. For that we need to choose a symmetric Gaussian surface passing through the point of interest. Then on applying the Gauss’s theorem on the surface, we will get the electric field.

Formula Used:
$\oint {EdS} = \dfrac{{{q_{enc}}}}{{{\varepsilon _0}}}$, where $E$ is the electric field, ${q_{enc}}$ is the charge enclosed within the Gaussian surface, and ${\varepsilon _0}$ is the electrical permittivity.

Complete step by step answer
According to the question, we have to determine the electric field at a point located outside the sphere of radius $a$ at a distance of $r$ from its centre. For determining the electric field, we use the Gauss theorem which is stated as
$\oint {EdS} = \dfrac{{{q_{enc}}}}{{{\varepsilon _0}}}$ …………………...(1)
Before applying the gauss theorem, we have to choose a suitable Gaussian surface which is symmetric around the charge distribution, passing through the point of interest. This is as shown in the below figure.

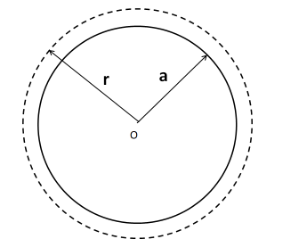
So the Gaussian surface is a sphere of radius $r$ concentric with the charged sphere.
Now, we evaluate the LHS of the equation (1)
$LHS = \oint {EdS}$
As the Gaussian surface is symmetric about the charge distribution, so the electric field is constant over the whole surface. So $E$ can be taken outside the integral
$LHS = E\oint {dS}$
$LHS = ES$
Putting the value of the surface area of the Gaussian sphere
$LHS = E\left( {4\pi {r^2}} \right)$
So (1) becomes
$E\left( {4\pi {r^2}} \right) = \dfrac{{{q_{enc}}}}{{{\varepsilon _0}}}$ …………………...(2)
Now we calculate the net charge enclosed within the Gaussian surface.
As can be clearly seen in the above, the Gaussian surface encloses the whole of the charged sphere. So, the net charge enclosed by the Gaussian surface is equal to the total charge on the sphere. That is, ${q_{enc}} = Q$ …………………...(3)
Putting (3) in (2) we have
$E\left( {4\pi {r^2}} \right) = \dfrac{Q}{{{\varepsilon _0}}}$
$\Rightarrow E = \dfrac{Q}{{4\pi {\varepsilon _0}{r^2}}}$
Thus the electric field outside the sphere is equal to $\dfrac{Q}{{4\pi {\varepsilon _0}{r^2}}}$.

Hence, the correct answer is option A.

Note
The expression for the electric field which comes out is similar to the electric field produced by a point charge. Hence a charged sphere behaves as a point charge concentrated at its centre for all the points on or outside its surface. So it must be remembered as a theorem to solve these kinds of questions quickly.