Question

Determine the coordinates of the point where the tangents drawn at the points to the parabola ${y^2} = 4x$ meet.

Answer 1

Hint : First we will find the equation of a tangent to parabola. Then we will find the value of a. now we know that since the tangent at the point must satisfy the equation of tangent. So from those two points we will find the equations on solving which we will get the point where the tangents meet.

Complete step by step solution:
Given the equation of parabola is ${y^2} = 4x$
General equation of parabola is ${y^2} = 4ax$
On comparing we get, $4a = 4$
And thus the value of a is $a = 1$
Now we know that the equation of tangent to parabola is given by,
$y{y_1} = 2a\left( {x + {x_1}} \right)$
But the value of a is 1. So the equation becomes,
$y{y_1} = 2\left( {x + {x_1}} \right)$
Now we will put the coordinates of the two points given in the equation above one by one,
Point $\left( {1,2} \right)$
Now putting the values of x and y,
$2y = 2\left( {x + 1} \right)$
Dividing both sides by 2 we get,
$y = x + 1$ ……eq1
Point $\left( {4,4} \right)$
Now putting the values of x and y,
$4y = 2\left( {x + 4} \right)$
Dividing both sides by 2 we get,
$2y = x + 4$ …..eq2
Now from eq1 and eq2 we will find the value of coordinates of the point where the tangents meet.
Eq2-eq1,
$2y - y = x + 4 - x - 1$
On subtracting we get,
$y = 4 - 1$
Then value of y is, $y = 3$
Putting this value in eq1 we get,
$x = y - 1$
Then,
$x = 3 - 1$
On subtracting we get,
$x = 2$
Thus the point where the tangents meet is $\left( {2,3} \right)$

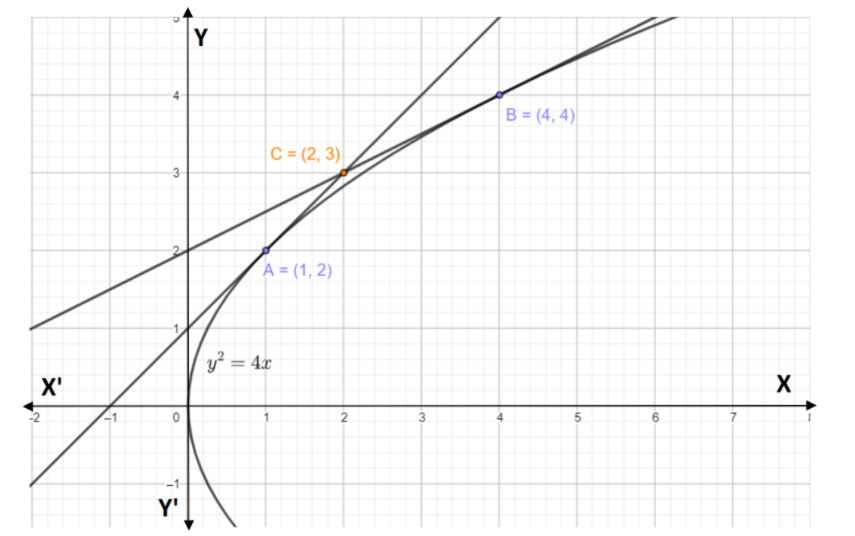
Note : We know the equation of tangent to parabola. Thus that is the only thing that will help in proceeding with the problem. Also note that the point where tangents meet need not to satisfy the equation of the parabola. This can be asked in like multiple and generally we tick yes, but it is not given that the point is on the parabola.