Question
Question: Determine the area under the curve \(y=\sqrt{{{a}^{2}}-{{x}^{2}}}\), included between the lines x= 0...
Determine the area under the curve y=a2−x2, included between the lines x= 0 and x= 4
Solution
Hint: Find the area in two different cases. When a is less than 4 and when a is greater or equal to 4. Observe that when a is less than 4, the whole curve in the domain x=0 to x= a will be included and the abscissae after x=a will be out from the domain. When a is greater or equal to 4, the whole curve in the domain x=0 to x= 4 will be included. Use the fact that the area of the region bounded by the curve y=f(x), the x-axis and the ordinates x=a and x=b is given by A=∫ab∣f(x)∣dx. Hence find the required area in the two different cases.
Complete step-by-step answer:
The above question can be solved in two cases:
Case I a≤4:
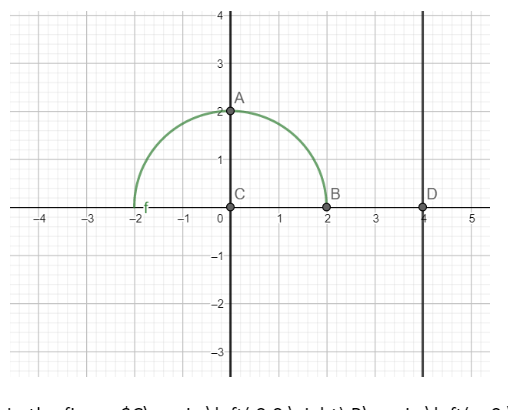
In the figure C≡(0,0),B≡(a,0) and D≡(4,0)
When a≤4, we have x∈(a,4] i.e. from B to D will be outside the domain. Hence when finding the area bounded by the curve y=a2−x2 , the x-axis and the ordinates x= 0 and x= 4, we will include the whole curve between x= 0 and x= a., i.e. the area of the region ABCA.
Hence the area will be the area bounded by y=a2−x2, the x-axis and the ordinates x= 0 and x =a
We know that the area of the region bounded by the curve y=f(x), the x-axis and the ordinates x=a and x=b is given by A=∫ab∣f(x)∣dx.
Hence, we have A=∫0aa2−x2dx
Since x≥0, we have
A=∫0aa2−x2dx
Put x=asint
Differentiating both sides with respect to t, we get
dx=acostdt
When x= 0, we have asint=0⇒t=0
When x= a, we have asint=a⇒a=2π
Hence, we have A=∫0aa2−a2sin2tacostdt=∫02πa2cos2tdt
Now, we know that ∫cos2tdt=∫21+cos2tdt=2t+4sin2t+C
Hence, we have
A=a22t+4sin2t02π=4πa2
Case II: When a≥4
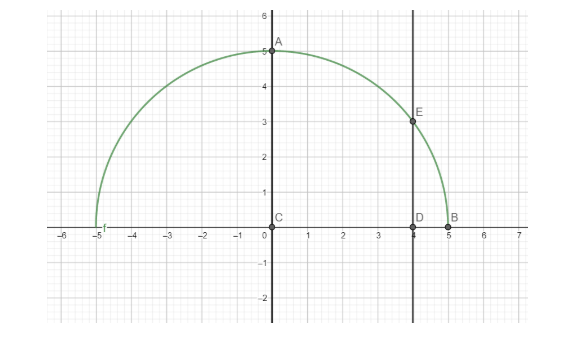
In this case, the required area is AEDCA, which is the area bounded by the curve y=a2−x2, the x-axis and the ordinates x=0 and x=4
We know that the area of the region bounded by the curve y=f(x), the x-axis and the ordinates x=a and x=b is given by A=∫ab∣f(x)∣dx.
Hence, we have
A=∫04a2−x2
Put x=asint
Differentiating both sides with respect to t, we get
dx=acostdt
When x= 0, we have asint=0⇒t=0
When x= 4, we have asint=4⇒a=sin−1a4
Hence, we have
A=a2∫0sin−1a4cos2t
Now, we know that ∫cos2tdt=∫21+cos2tdt=2t+4sin2t+C
Hence, we have
A=a22t+4sin2t0sin−1a4=a22sin−1a4+4sin(2sin−1a4)
We know that sin(2x)=2sinxcosx
Hence, we have
sin(2sin−1ax)=2sin(sin−1a4)cos(sin−1a4)
We know that cos(sin−1a4)=1−(a4)2
Hence, we have sin(2sin−1a4)=a81−(a4)2
Hence, we have
A=a22sin−1a4+4a81−(a2)2=a22sin−1a4+a21−(a4)2=2a2sin−1a4+2a2−16
Note: Alternatively in case I, the value of A can be found by observing that it is the area of a quarter of a circle of radius and hence is equal to 4πa2 and in the case II, the value of A can be found by using the property that ∫a2−x2dx=2xa2−x2+2a2sin−1ax
Hence, we have
A=2xa2−x2+2a2sin−1ax04=2a2−16+2a2sin−1a4, which is the same as obtained above.
