Question

Determine graphically whether the system of equations$x-2y=2,4x-2y=5$ is consistent or inconsistent.

Answer 1

Hint: First draw the graph of the two given equations. To draw the graph of a straight line, we need at least two points. So, choose one of the equations and substitute x = 0, determine y, then substitute y = 0, determine x. Now, apply the same process for the second equation. Plot the graph of the two equations using the points obtained. Now, if the graphs of these equations are parallel to each other then the system of equations is inconsistent and if they are intersecting at a particular point then they are consistent.

Complete step-by-step answer:

Let us assume the two equations as:

& x-2y=2....................(i) \\\ & 4x-2y=5..................(ii) \\\ \end{aligned}$$ Considering equation (i), $$x-2y=2$$ Substituting x = 0, we get, $$\begin{aligned} & -2y=2 \\\ & \Rightarrow y=-1 \\\ \end{aligned}$$ Substituting y = 0, we get, $x=2$ Therefore, the two points are: $A\left( 2,0 \right)\text{ and }\left( 0,-1 \right)$. Considering equation (ii), $$4x-2y=5$$ Substituting x = 0, we get, $\begin{aligned} & -2y=5 \\\ & \Rightarrow y=\dfrac{-5}{2} \\\ \end{aligned}$ Substituting y = 0, we get, $\begin{aligned} & 4x=5 \\\ & \Rightarrow x=\dfrac{5}{4} \\\ \end{aligned}$ Therefore, the two points are: $C\left( \dfrac{5}{4},0 \right)\text{ and }D\left( 0,\dfrac{-5}{2} \right)$. Therefore, the graph of the two functions can be plotted as: 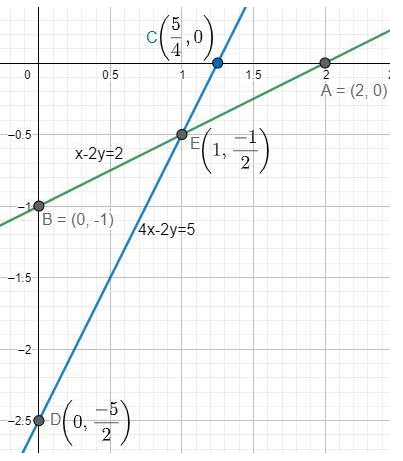 Clearly, we can see that the two lines are intersecting each other at a particular point E. To determine this point of intersection, we have to solve the equations algebraically. Let us solve the two equations. Subtracting equation (i) from equation (ii), we get, $\begin{aligned} & 3x=3 \\\ & \Rightarrow x=1 \\\ \end{aligned}$ Substituting (x = 1) in equation (i), we get, $\begin{aligned} & 1-2y=2 \\\ & \Rightarrow 2y=-1 \\\ & \Rightarrow y=\dfrac{-1}{2} \\\ \end{aligned}$ Therefore, the intersection point is given by: $E\left( 1,\dfrac{-1}{2} \right)$. Hence, the system of equations is consistent (i.e. has a unique solution). Note: There is another method to check the consistency or inconsistency of a system of equations without the use of graph. To apply this method, write the two equations in the form: ${{a}_{1}}x+{{b}_{1}}y+{{c}_{1}}=0$ and ${{a}_{2}}x+{{b}_{2}}y+{{c}_{2}}=0$ respectively. Now, consider the ratios: $\dfrac{{{a}_{1}}}{{{a}_{2}}},\dfrac{{{b}_{1}}}{{{b}_{2}}}\text{ and }\dfrac{{{c}_{1}}}{{{c}_{2}}}$. From here, three cases can arise: Case (i): If $\dfrac{{{a}_{1}}}{{{a}_{2}}}\ne \dfrac{{{b}_{1}}}{{{b}_{2}}}$ then the system has unique solution. Case (ii): If $\dfrac{{{a}_{1}}}{{{a}_{2}}}=\dfrac{{{b}_{1}}}{{{b}_{2}}}\ne \dfrac{{{c}_{1}}}{{{c}_{2}}}$ then the system has no solution. Case (iii): If $\dfrac{{{a}_{1}}}{{{a}_{2}}}=\dfrac{{{b}_{1}}}{{{b}_{2}}}=\dfrac{{{c}_{1}}}{{{c}_{2}}}$ then the system has infinitely many solutions. As we can see that the above question has a situation of case (i). Therefore, the system of equations has a unique solution.