Question
Question: Describe the motion of the charge particle when it is displaced along the x-axis. Also, find its acc...
Describe the motion of the charge particle when it is displaced along the x-axis. Also, find its acceleration.
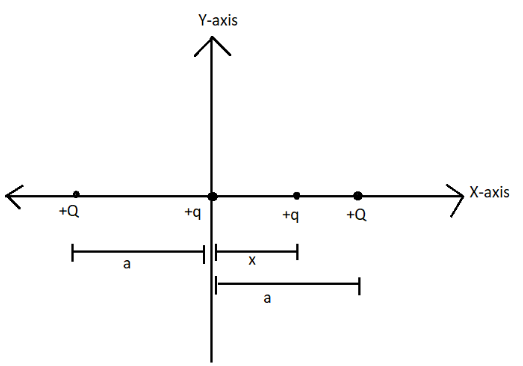
Solution
The formula for Newton's second law of motion is applied along with the formula for Lorentz force and these two equations of force are equated and rearranged to get the equation for acceleration. Since there is no magnetic field, only the formula based on the electrostatic force applied on a charged particle is taken into consideration and equated with the formula for Newton's second law of motion to get the acceleration which can then be substituted in the straight line of motion equation for displacement.
Complete step by step answer:
When a charged particle is placed on the x-axis in the presence of two other charge particles (as shown in the diagram) then it experiences a force and due to this force it will be displaced. Forces can be due to two fields; it can be either electric field or magnetic field. It is imperative to determine the field which is present in the region of the charged particle because the force applied by the electric or the magnetic field is responsible for the motion or the displacement of the charged particle from its original position.
The determination of the presence of electric field or magnetic field is found out in-order to describe its motion.When there is a presence of a charged particle in the region of one or more point charges an electric field is definitely produced (in accordance to Coulomb’s law). From the diagram, it can be observed that q is the test charge.
The electrostatic force applied on the test charge by a point charge separated by a distance is given by a formula. This formula is given by the Lorentz force in an electric field.
F=E×q ---(1)
where, F is the Coulomb or the electrostatic force, E is the electric field and q is the test charge.
Since E is a vector quantity and hence it has magnitude as well as direction. The direction of motion of the charged particle or the displacement of the charged particle is always said to be in the direction of the applied electric field when the magnitude of the charged particle is positive. According to Newton's second law of motion the acceleration depends upon the net force exerted on the particle and the mass remains constant. The formula is as follows:
F=m×a ----(2)
where, F is the net force on the particle, a is the acceleration and m is the mass of the particle.
Since equations (1) and (2) are identical they are equated to find the value of acceleration.
ma=Eq
⇒a=mEq ----(3)
Now we determine whether there is a presence of magnetic force on the particle. This is given by the Lorentz force formula:
F=qvB ----(4)
where, F is the Lorentz force, q is the charge of the particle, v is the velocity of the particle and B is the magnetic field.
Now equations (2) and (4) are equated as they are similar. We get:
ma=qvB
The equation for acceleration is then determined.
⇒a=mqvB
But the value of B , that is the magnetic field, is zero because the velocity and the magnetic field are in the same direction, that is they are parallel. A charge moving in parallel to the direction of the magnetic field does not experience any magnetic force.Hence acceleration becomes zero since there is no presence of magnetic force and hence there is no motion (circular motion) due to the absence of magnetic field.
Hence the motion of the particle is linear and is displaced in the direction of the electric field. This displacement is given by the equation of straight line of motion:
x=v0t+21at2----(5)
where, x is the displacement, v0 is the velocity along the x-direction and t is the time taken.
The acceleration of the particle is hence only due to the electric field and from equation (3) it is given by:
a=mEq
Substituting this value in equation (5) we get:
∴x=v0t+2mqEt2
Hence the displacement or the motion of the particle is given by the above value.
Additional information: Lorentz force is the force experienced by a charged particle moving in a region where both electric and magnetic fields are present. This force with respect to the electric field, does not depend on the velocity of the charge but in the case of an applied magnetic field it depends on the velocity. If in a field, the moving charge experiences a force depending upon the strength of the field and not on its velocity then there is a presence of electric field or else there is a presence of magnetic field.
Note: There can be a misconception when considering which forces to take into consideration. Both electric and magnetic fields must be considered. Thus, it is essential to check for the presence of which fields are applied to the charged particle due to which there is motion.
