Question

Describe Kelvin’s method to determine the resistance of the galvanometer by using Meter Bridge.

Answer 1

Meter Bridge in a balanced condition gives the value of unknown resistance. In Meter Bridge, the balance point is obtained at the middle of the meter bridge wire.

Complete step by step answer:
The meter bridge is the practical form of Wheatstone bridge.
The working principle states that at any point of length of wire, if the ratio of two resistances are equal to that of the ratio of other two resistances, then no current flows through that point, that is, the galvanometer point shows no deflection.

In order to describe Kelvin’s method to determine resistance of the galvanometer, we need the following set up:
Here, we have:
(a) A galvanometer whose resistance is to be calculated (connected in one gap) denoted as ${G_R}$
(b) A variable known resistance (connected in the other gap) denoted as R
(c) A rheostat that can provide variable resistance
(d) A cell emf
(e) The point between the galvanometer and the variable resistance is directly connected to the jockey
(f) A switch.

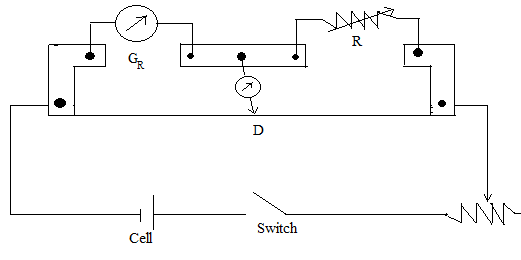
The switch is closed, and the power supply is switched on, so that current flows in the circuit.
The maximum value of resistance (R) is taken from the resistance box, and the value of rheostat resistance is decreased gradually.
Then the jockey slides over the meter bridge points at the two extreme edges, and checks if the galvanometer shows deflection on both sides.
Now, the jockey is slid to such a point, where the galvanometer shows no deflection. This point is called the balance point.
The length of the wire opposite to the galvanometer is noted as ${L_G}$and the length of the wire, opposite to the resistance box is noted as${L_R}$; as shown in the figure.
Applying the equation for balanced bridge condition:
$\dfrac{{{G_R}}}{R} = \dfrac{{\lambda {L_G}}}{{\lambda {L_R}}}$
Where,
$\lambda$is the resistance per unit length of the wire.
Thus the equation becomes:
${G_R} = R\dfrac{{{L_G}}}{{{L_R}}}$
Thus, the resistance of the galvanometer can be obtained.

Note: Readings should be taken very carefully, otherwise the obtained value will be erroneous. $\lambda$ gets cancelled because in calculations as, for the same wire, resistance per unit length is constant.
This is to be kept in mind that since we knew the resistance per length of the wire, calculating the respective lengths on either side of the balance point, helped us to get the required value of resistances.