Question

Describe Kelvin’s method to determine the resistance of a galvanometer by using a meter bridge.

Answer 1

Kelvin’s method determines the resistance of the galvanometer using the principle of Wheatstone bridge, which makes it easier to find the resistance since you only need to know the ratio of the lengths and not the specific value of resistance of wires.

Complete step by step answer:
Kelvin’s method is one of the most popular and easiest methods to determine the resistance of a galvanometer. Let’s explain to you why is it so:
This is how we use the Kelvin’s method to find the resistance of a galvanometer:
These are the steps to determine the resistance of the galvanometer:

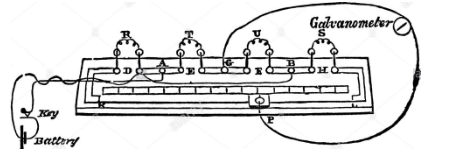
1. Connect Galvanometer $G$ in the left gap and resistance box $R$ in the right gap.
2. Battery, key and rheostat are connected in series. Common junction of $G$ and R is connected to the jockey.
3. Take resistance $R$ from the box and close the key so that current can flow through the circuit.
4. Without touching the jockey at any point on the wire, note the reading of $G$ .
5. Now touch the jockey on the different points of the wire and find the point at which $G$ gives the same reading as before when the jockey has no contact with the wire.
6. Let D is the point at which reading was same
   Now, according to the balanced wheatstone bridge concept:
   $\dfrac{G}{R} = \dfrac{{AD}}{{CD}}$
   Let us assume that $\sigma$ is the resistivity of the wire
   Let us assume the length of AD be $L$
   We will assume the length of CD to be $l$
   Since the total length of the wire is $100\,cm$ , we can see that:
   $l = 100 - L$
   Now, substituting the values, we get:

$$\dfrac{G}{R} = \dfrac{{\sigma L}}{{\sigma l}} \\\ \dfrac{G}{R} = \dfrac{L}{{100 - L}} \\\ G = R\left( {\dfrac{L}{{100 - L}}} \right) \\\$$

And thus, we found out the value of the resistance of the galvanometer so easily.

Note: Many students forget that wheatstone bridge is just a condition or specific arrangement and can be used on an arrangement of any wire. This is what is used in Kelvin's method and this is what makes the determination of the resistance of the galvanometer so simple and easy.