Question

Derive the third equation of the motion-

Answer 1

The third equation of motion is the relationship between final velocity ‘v’, initial velocity ‘u’ , acceleration ‘and distance travelled ‘s’. We will start by considering that a body is moving with uniform acceleration. We will plot the v-t (velocity-time) graph for the body and using the graph we will reach the equation.

Complete step-by-step solution:
Let us first know a few terms:

1. initial velocity is the velocity with which the body first starts moving.
2. final velocity- velocity the body attains after completing its motion.
   Let us start by considering a body, moving on a plane with uniform acceleration ’a’. let ‘u’ be its initial velocity ’v’ be its final velocity, ‘t’ be time travelled and ‘s’ be distance travelled. And ‘a’ is the acceleration .
   We will plot a( v-t) graph to derive this equation:
   Look at the following graph,
   
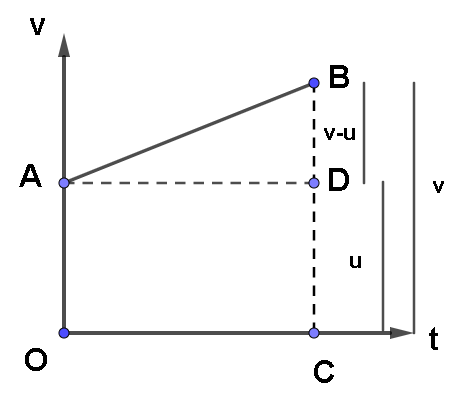
   Here: OA=CD=u
   BC=v
   AND, OC=AD=t
   As total height is v, then the height BD=BC-BD.
   That is BD=v-u
   We know that the slope of the v-t graph gives acceleration.
   Hence, $a = \dfrac{{BD}}{{AD}}$
   $a = \dfrac{{BC - CD}}{{OC}}$
   $a = \dfrac{{v - u}}{t}$
   $t = \dfrac{{v - u}}{a} - - - - - - - - - - - \left( 1 \right)$
   Distance travelled by the body in time t= area enclosed by v-t graph.
   We see that there is a trapezium formed with height ‘t’ and sum of parallel sides as ‘u’ and ‘v’ .
   Hence the distance travelled by the body =area of the trapezium in the graph.
   X=area of trapezium
   $x = \dfrac{1}{2} \times OC \times \left( {OA + BC} \right)$
   $x = \dfrac{1}{2} \times t \times \left( {u + v} \right)$
   Now substituting value of t from equation 1, we get
   $x = \dfrac{1}{2} \times \left( {\dfrac{{v - u}}{a}} \right) \times \left( {u + v} \right)$
   $x = \dfrac{1}{{2a}} \times \left( {v - u} \right) \times \left( {u + v} \right)$
   $x = \dfrac{1}{{2a}} \times \left( {{v^2} - {u^2}} \right)$
   Or, $x2a = \left( {{v^2} - {u^2}} \right)$
   Substituting x=s we get :
   $2as = \left( {{v^2} - {u^2}} \right)$
   $\therefore {v^2} = {u^2} + 2as$
   Hence derived.

Note: The slope under the (v-t) graph gives acceleration.
The area under the curve of a (v-t) graph gives the displacement.
Remember to write BD=v-u , otherwise the whole derivation could go wrong.
Also all the equations of motion can be applied only when the acceleration is constant.