Question

Derive the thin lens formula.

Answer 1

Hint: Try to learn about different types of lenses. Learn the concepts of image formation using lenses. Then apply this concept to a thin convex lens and do the formation image part by part to obtain a thin lens formula.

Complete step by step answer:
Consider a thin convex lens.

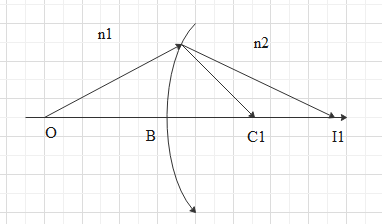
Let the first reflecting surface of the lens form an image at ${{I}_{1}}$ of object at O.
Relation between the object and image distance in terms of the refractive index can be given as,
$\dfrac{{{n}_{1}}}{OB}+\dfrac{{{n}_{2}}}{B{{I}_{1}}}=\dfrac{{{n}_{2}}-{{n}_{1}}}{B{{C}_{1}}}\text{ }\to \text{ 1}$
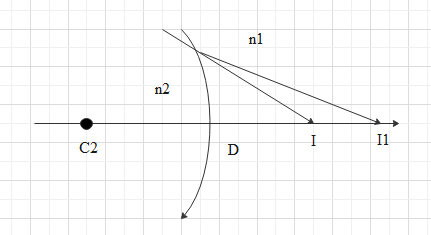
The image at ${{I}_{1}}$ acts as a virtual object for the second surface of the lens and it will form an image at $I$.
$-\dfrac{{{n}_{2}}}{D{{I}_{1}}}+\dfrac{{{n}_{1}}}{DI}=\dfrac{{{n}_{2}}-{{n}_{1}}}{D{{C}_{2}}}\text{ }\to \text{ 2}$
Now, for a thin lens we will get $B{{I}_{1}}\cong D{{I}_{1}}$
Putting this value on equation 1 and 2, and then adding the two equations, we get,

$\begin{aligned} & \dfrac{{{n}_{1}}}{OB}+\dfrac{{{n}_{2}}}{B{{I}_{1}}}-\dfrac{{{n}_{2}}}{B{{I}_{1}}}+\dfrac{{{n}_{1}}}{DI}=\dfrac{{{n}_{2}}-{{n}_{1}}}{B{{C}_{1}}}\text{+}\dfrac{{{n}_{2}}-{{n}_{1}}}{D{{C}_{2}}}\text{ } \\\ & \dfrac{{{n}_{1}}}{OB}+\dfrac{{{n}_{1}}}{DI}=\left( {{n}_{2}}-{{n}_{1}} \right)\left( \dfrac{1}{B{{C}_{1}}}\text{+}\dfrac{1}{D{{C}_{2}}} \right)\text{ }\to \text{ 3} \\\ \end{aligned}$
Now, suppose the object is at infinity, i.e. $OB\to \infty$ and $DI=f$ , then we can write the above equation as,
$\begin{aligned} & \dfrac{{{n}_{1}}}{\infty }+\dfrac{{{n}_{1}}}{f}=\left( {{n}_{2}}-{{n}_{1}} \right)\left( \dfrac{1}{B{{C}_{1}}}\text{+}\dfrac{1}{D{{C}_{2}}} \right) \\\ & \dfrac{{{n}_{1}}}{f}=\left( {{n}_{2}}-{{n}_{1}} \right)\left( \dfrac{1}{B{{C}_{1}}}\text{+}\dfrac{1}{D{{C}_{2}}} \right)\text{ }\to \text{ 4} \\\ \end{aligned}$

Comparing equation 3 and 4 we get that,
$\begin{aligned} & \dfrac{{{n}_{1}}}{OB}+\dfrac{{{n}_{1}}}{DI}=\dfrac{{{n}_{1}}}{f} \\\ & \dfrac{1}{OB}+\dfrac{1}{DI}=\dfrac{1}{f} \\\ \end{aligned}$
Again, in thin lens approximation we can say that B and D are both close to the optical centre of the lens. Applying the sign convention, we can write,
$BO=-u\text{ and }DI=+v$
Where, u is the object distance and v is the image distance.
So, the above equation can be written as,
$\begin{aligned} & \dfrac{1}{-u}+\dfrac{1}{v}=\dfrac{1}{f} \\\ & \dfrac{1}{v}-\dfrac{1}{u}=\dfrac{1}{f} \\\ \end{aligned}$
This is the thin lens formula.

Note: Here, we have derived the thin lens formula considering the image formation process in a convex lens. But this formula is also valid for the concave lens for both real and virtual images.
In a spherical mirror we have two focal points. These two focal points are equidistant from the mirrors optical centre.