Question

Derive the relation $a\sin \theta = \lambda$ for the first minimum of the diffraction pattern produced due to a single slit of width ‘ $a$ ’ using light of wavelength $\lambda$.

Answer 1

First minima means $n = 1$.
Intensity at secondary minima at $\theta = \dfrac{{n\lambda }}{a}$

Complete step by step solution:

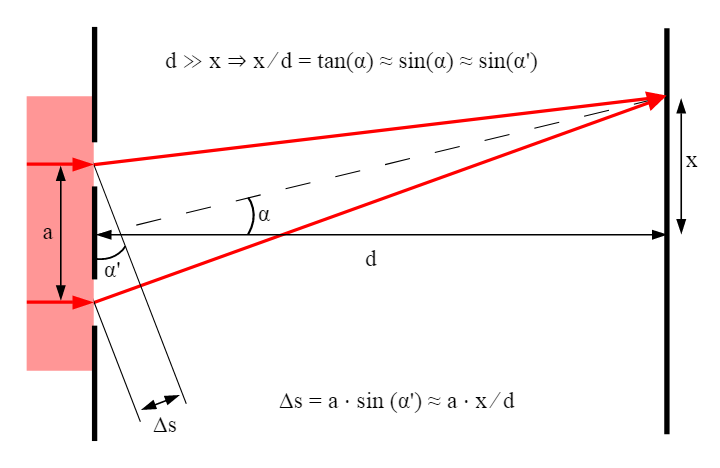
Let us consider a point P on screen.
We know, path difference is the difference in distance travelled by the two waves from their source to a particular point on screen. Therefore, path difference at point p denoted by$\Delta x$.

From the diagram it is evident that $\Delta x = BC$
Considering $\Delta ABC$,
We know, $\sin \theta = \dfrac{{perpendicular}}{{hypotenuse}}$
Where: a= width of the slit
$\Delta x$= phase difference

Therefore, from the diagram we get: $\sin \theta = \dfrac{{BC}}{{AB}} = \dfrac{{\Delta x}}{a}$
Rearranging the equations we get,
$\Delta x = a\sin \theta$

We know, due to experimental results we obtain,
Intensity at minima is given by $\theta = \dfrac{{n\lambda }}{a}$

Where, n= the number of fringe
$\lambda$= wavelength of light used
a= width of the slit
For very small value of $\theta$, we consider $\theta \approx \sin \theta$,
And we know,
$\theta = \dfrac{{n\lambda }}{a}$
Therefore, it can be implied that,
$\sin \theta = \dfrac{{n\lambda }}{a}$
Since, the question states first minima, we take n=1 and the equation becomes: $a\sin \theta = \lambda$
This is our required equation. Hence, proved.

Additional Information:
Diffraction is defined as the spreading of light waves when it passes through a narrow slit or an obstacle.
There are mainly two kinds of diffraction-
(i) Fraunhofer Diffraction
(ii) Fresnel Diffraction

Huygens’s principle states that each point of the wave front sends various wavelets in various directions, each of these wavelets superimpose on the screen to give rise to Diffraction.

Note: The question asks to find the expression for the first minima only.
When a monochromatic light is incident on a single slit, the light passing falls on the screen, and on superimposing, diffraction pattern is obtained.