Question

Derive the formula for the volume of a cone, given to you in the figure using the symbols as explained.

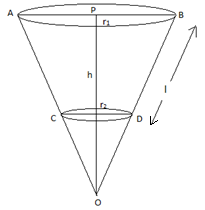
h = height of frustum
l = slant height of frustum
${{r}_{1}}$ = radius PB
${{r}_{2}}$ = radius QD

Answer 1

Hint: We will assume the height of the cone, slant height of the cone OCD also its slant height to be a variable. Then we will write these variables into the given variables in the question. To calculate the volume of frustum, we will subtract the volume of the cone OCD from the volume of the cone AOB.

Complete step-by-step answer:
We have been given the height of the frustum (h), radius of upper part (${{r}_{1}}$), slant height (l) and radius of lower part of frustum (${{r}_{2}}$) as shown in the figure.

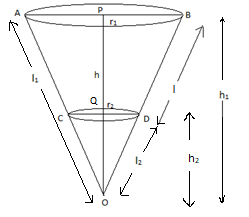
Now let us assume $OP={{h}_{1}},OQ={{h}_{2}},OD={{l}_{2}},OA={{l}_{1}}$.
From the above figure, we can observe that OA = OC + AC.
We can see that OC = OD = ${{l}_{2}}$ and AC = BD = $l$. So we can substitute it as,
$\Rightarrow {{l}_{1}}={{l}_{2}}+l.....(1)$
Also, OP = OQ + PQ
$\Rightarrow {{h}_{1}}={{h}_{2}}+h.....(2)$
As we know that the volume of frustum is equal to the difference between the cone OAB and cone OCD.
$\Rightarrow$Volume of frustum = volume of cone OAB – volume of cone OCD
We know that if a cone has radius and height r and h respectively, then its volume is as follows:
$\Rightarrow$Volume of cone $=\dfrac{1}{3}\pi {{r}^{2}}h$
$\Rightarrow$Volume of cone OAB $=\dfrac{1}{3}\pi {{r}_{1}}^{2}{{h}_{1}}$
Now in $\Delta OPB$ and $\Delta OQD$,
$\angle BOP=\angle DOQ$
As both angles are common to the triangles
$\angle OPB=\angle OQD$
Since both angles are ${{90}^{\circ }}$ as height are perpendicular
$\Rightarrow \Delta OPB\sim \Delta OQD$ by AA angle similarity
As we know that the corresponding sides of a similar triangle are proportional,

& \Rightarrow \dfrac{PB}{QD}=\dfrac{OB}{OD} \\\ & \Rightarrow \dfrac{{{r}_{1}}}{{{r}_{2}}}=\dfrac{{{h}_{1}}}{{{h}_{2}}} \\\ \end{aligned}$$ On substituting $${{h}_{1}}=h+{{h}_{2}}$$ from equation (2), we get as follows: $$\begin{aligned} & \Rightarrow \dfrac{{{r}_{1}}}{{{r}_{2}}}=\dfrac{{{h}_{1}}}{{{h}_{2}}} \\\ & \Rightarrow \dfrac{{{r}_{1}}}{{{r}_{2}}}=\dfrac{h+{{h}_{2}}}{{{h}_{2}}} \\\ & \Rightarrow \dfrac{{{r}_{1}}}{{{r}_{2}}}=\dfrac{h}{{{h}_{2}}}+\dfrac{{{h}_{2}}}{{{h}_{2}}} \\\ & \Rightarrow \dfrac{{{r}_{1}}}{{{r}_{2}}}=\dfrac{h}{{{h}_{2}}}+1 \\\ & \Rightarrow \dfrac{{{r}_{1}}}{{{r}_{2}}}-1=\dfrac{h}{{{h}_{2}}} \\\ & \Rightarrow \dfrac{{{r}_{1}}-{{r}_{2}}}{{{r}_{2}}}=\dfrac{h}{{{h}_{2}}} \\\ \end{aligned}$$ On cross multiplication, we get as follows: $$\begin{aligned} & \Rightarrow \left( {{r}_{1}}-{{r}_{2}} \right){{h}_{2}}=h{{r}_{2}} \\\ & \Rightarrow {{h}_{2}}=h\left( \dfrac{{{r}_{2}}}{{{r}_{1}}-{{r}_{2}}} \right).....(2) \\\ \end{aligned}$$ So after using the value of $${{h}_{2}}$$ in the volume of frustum, we get as follows: Volume of frustum $$=\dfrac{1}{3}\pi {{r}_{1}}^{2}{{h}_{1}}-\dfrac{1}{3}\pi {{r}_{2}}^{2}{{h}_{2}}=\dfrac{1}{3}\pi {{r}_{1}}^{2}{{h}_{1}}-\dfrac{1}{3}\pi {{r}_{2}}^{2}h\left( \dfrac{{{r}_{2}}}{{{r}_{1}}-{{r}_{2}}} \right)$$ We know that $${{h}_{1}}=h+{{h}_{2}}$$, so by substituting the value of $${{h}_{1}}$$ we get as follows: Volume of frustum $$=\dfrac{1}{3}\pi {{r}_{1}}^{2}\left( h+{{h}_{2}} \right)-\dfrac{1}{3}\pi {{r}_{2}}^{2}h\left( \dfrac{{{r}_{2}}}{{{r}_{1}}-{{r}_{2}}} \right)$$ $$\begin{aligned} & =\dfrac{1}{3}\pi {{r}_{1}}^{2}\left( h+h\left( \dfrac{{{r}_{2}}}{{{r}_{1}}-{{r}_{2}}} \right) \right)-\dfrac{1}{3}\pi {{r}_{2}}^{2}h\left( \dfrac{{{r}_{2}}}{{{r}_{1}}-{{r}_{2}}} \right) \\\ & =\dfrac{1}{3}\pi {{r}_{1}}^{2}h\left( 1+\dfrac{{{r}_{2}}}{{{r}_{1}}-{{r}_{2}}} \right)-\dfrac{1}{3}\pi {{r}_{2}}^{2}h\left( \dfrac{{{r}_{2}}}{{{r}_{1}}-{{r}_{2}}} \right) \\\ & =\dfrac{1}{3}\pi {{r}_{1}}^{2}h\left( \dfrac{{{r}_{1}}-{{r}_{2}}+{{r}_{2}}}{{{r}_{1}}-{{r}_{2}}} \right)-\dfrac{1}{3}\pi {{r}_{2}}^{2}h\left( \dfrac{{{r}_{2}}}{{{r}_{1}}-{{r}_{2}}} \right) \\\ & =\dfrac{1}{3}\pi {{r}_{1}}^{2}h\left( \dfrac{{{r}_{1}}}{{{r}_{1}}-{{r}_{2}}} \right)-\dfrac{1}{3}\pi {{r}_{2}}^{2}h\left( \dfrac{{{r}_{2}}}{{{r}_{1}}-{{r}_{2}}} \right) \\\ & =\dfrac{1}{3}\pi h\left( \dfrac{{{r}_{1}}^{3}}{{{r}_{1}}-{{r}_{2}}} \right)-\dfrac{1}{3}\pi h\left( \dfrac{{{r}_{2}}^{3}}{{{r}_{1}}-{{r}_{2}}} \right) \\\ \end{aligned}$$ Taking $$\dfrac{1}{3}\pi h$$ as common, we get as follows: Volume of frustum $$=\dfrac{1}{3}\pi h\left( \dfrac{{{r}_{1}}^{3}-{{r}_{2}}^{3}}{{{r}_{1}}-{{r}_{2}}} \right)$$ We know that $${{a}^{3}}-{{b}^{3}}=\left( a-b \right)\left( {{a}^{2}}+{{b}^{2}}+ab \right)$$ Volume of frustum $$=\dfrac{1}{3}\pi h\dfrac{\left( {{r}_{1}}-{{r}_{2}} \right)\left( {{r}_{1}}^{2}+{{r}_{2}}^{2}+{{r}_{1}}{{r}_{2}} \right)}{\left( {{r}_{1}}-{{r}_{2}} \right)}$$ $$=\dfrac{1}{3}\pi h\left( {{r}_{1}}^{2}+{{r}_{2}}^{2}+{{r}_{1}}{{r}_{2}} \right)$$ Hence the formula for the volume of the frustum of a cone is derived to be $$\dfrac{1}{3}\pi h\left( {{r}_{1}}^{2}+{{r}_{2}}^{2}+{{r}_{1}}{{r}_{2}} \right)$$. Note: Be careful while calculation and also take care of the algebraic sign as there is a chance of error after submitting the value of $${{h}_{1}}$$ and $${{h}_{2}}$$ in the equation of volume of frustum. Also remember the volume of frustum as formula.