Question
Question: Derive the formula for moment of inertia of a hoop with axis across the diameter....
Derive the formula for moment of inertia of a hoop with axis across the diameter.
Solution
To solve the questions related to moment of inertia of continuous distribution we consider the moment of inertia for an infinitesimal part of the body having infinitesimal mass and then integrate it for the whole body. To solve the integral, we consider the relation of infinitesimal mass with the mass of the whole body and try to convert the whole integral into known parameters.
Formula used:
Moment of inertia for continuous body is given by formula,
I=∫dm×r⊥
Where dm denotes the mass of the considered infinitesimal element and r⊥ is the perpendicular distance of the element from the axis of rotation.
Complete step by step answer:
Let us take the total mass of the hoop be M and radius be r. Now, consider a small element of mass dm at distance r′ from the axis of rotation as shown in the figure.
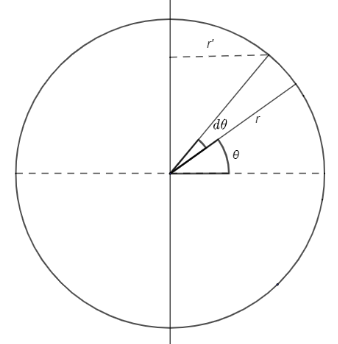
Moment of inertia for this small element is =dm×r′
Now, we will integrate it to get the moment of inertia for the whole hoop.
I=∫dm×r′
We will try to simplify the integral using-
dm=2πMdθ
Also, r′=rcosθ
Now, substitute these values in the integral and integrate-
I=0∫2π2πMdθ×(rcosθ)2
⇒I=2πMr20∫2πcos2θdθ
We know that, cos2θ=21+cos2θ, substitute this in previous equation and solve-
