Question

Derive the formula for equivalent capacitance when the capacitors are connected in series.

Answer 1

Hint
Two conducting plates separated by a distance is called a capacitor. On the application of current, the plates will get charged with the opposite charge. In a series connection, the capacitors are connected in an end to end connection. In a series connection, each capacitor will carry the same amount of charge.

Complete step by step answer
Consider a series combination of capacitors, where the capacitors are connected in an end to end connection as shown in the figure.

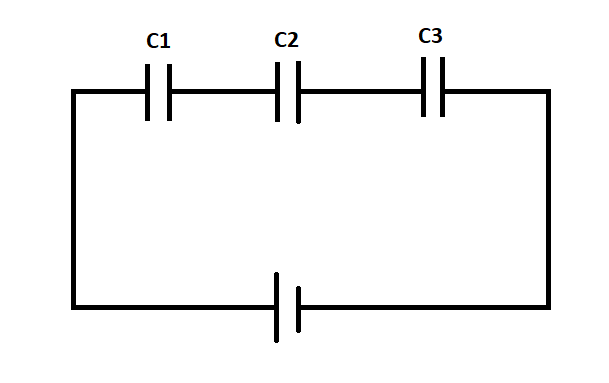
Let $V$ be the potential difference applied across the series combination. The one property that we have to take care of in a series combination is that each capacitor will have the same amount of charge.
Let the potential difference be, ${V_1},{V_2}$ and ${V_3}$ across the capacitors, ${C_1},{C_2}$ and ${C_3}$ respectively,
$\therefore$ We can write the applied potential as,
$\Rightarrow V = {V_1} + {V_2} + {V_3}$
The potential difference of each capacitor can be written as,
$\Rightarrow {V_1} = \dfrac{{{Q_1}}}{{{C_1}}},{V_2} = \dfrac{{{Q_2}}}{{{C_2}}}$ and ${V_3} = \dfrac{{{Q_3}}}{{{C_3}}}$
If we replace the combination of capacitors with a single capacitor, then we can write the effective resistance as,
$\Rightarrow V = \dfrac{Q}{C}$
Substituting equation and in equation we get,
$\Rightarrow \dfrac{Q}{C} = \left[ {\dfrac{{{Q_1}}}{{{C_1}}} + \dfrac{{{Q_2}}}{{{C_2}}} + \dfrac{{{Q_3}}}{{{C_3}}}} \right]$
From this we get the effective capacitance as,
$\Rightarrow \dfrac{1}{C} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}} + \dfrac{1}{{{C_3}}}$
Thus we get that, the reciprocal of the effective capacitance is equal to the sum of the reciprocal of the individual capacitances.

Note
In a series combination, the effective capacitance will be less than the lowest capacitance in the combination. Thus a series combination is used to reduce the effective capacitance. The effective capacitance in a parallel combination is higher than the highest value of capacitance in the combination. Thus a parallel combination is used to increase the effective capacitance of the circuit.