Question

Derive the following expression for the refraction at concave spherical surface:
$\dfrac{\mu }{v} - \dfrac{1}{u} = \dfrac{{\mu - 1}}{R}.$

Answer 1

Hint
A spherical mirror is a part of a sphere with a reflecting surface. If the inner surface is the reflective surface then the mirror is called a concave mirror and if the outer surface is the reflecting surface then the mirror is called a convex mirror. Here we have a concave reflecting surface for which we have to derive the given expression.

Complete step by step answer
Let us consider a concave mirror as shown in the diagram below,

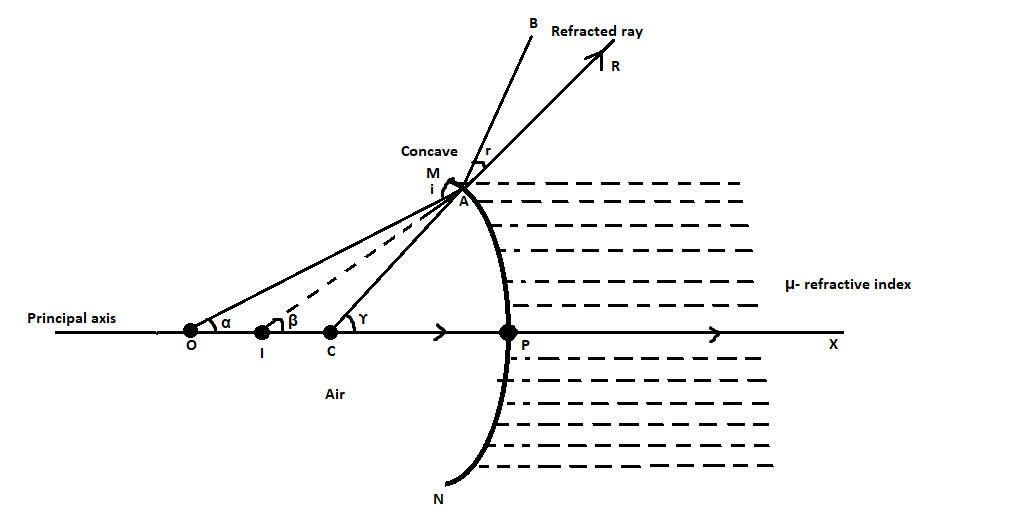
The concave mirror is represented by $MPN$ . The refractive index of the medium of the spherical surface is given by $\mu$ . We consider $P$ as the pole of the mirror, $O$ as the centre of curvature, and $PC$ represents the principal axis of the refractive spherical surface. We consider a point object at $O$ . An incident ray travels through $C$ and it is normal to the spherical surface. It will not undergo any refraction hence it will travel in a straight line along $PX$ . Another ray that we consider is $OA$ . It will refract at the point $A$ bending towards the normal. At a point $i$ we will get a virtual image.
Let us consider the ray angles with the principal axis to be $\alpha,\beta$ , and $\gamma$ respectively.
According to Snell’s law, we can write the refractive index as
$\Rightarrow \mu = \dfrac{{\sin i}}{{\sin r}}$
Where $i$ is the angle of incidence and $r$ is the angle of refraction.
Here we have very small $i$ and $r$ , hence we can write,
$\Rightarrow \sin i = i$ And $\sin r = r$ in equation
We get,
$\Rightarrow \mu = \dfrac{i}{r}$
From this we get,
$\Rightarrow i = \mu r$
By using the exterior angle theorem, from $\Delta AOC$ we get,
$\Rightarrow \gamma = i + \alpha$
From this we get
$\Rightarrow i = \gamma - \alpha$
Now, by using exterior angle theorem in $\Delta IAC$ , we get
$\Rightarrow \gamma = \beta + r$
From this we get,
$\Rightarrow r = \gamma - \beta$
Substituting these values of $i$ and $r$ in equation we get,
$\Rightarrow \left( {\gamma - \alpha } \right) = \mu \left( {\gamma - \beta } \right)$
For a spherical surface, we can write the angle as
$\Rightarrow angle = \dfrac{{arc}}{{radius}}$
We can write
$\Rightarrow \alpha = \dfrac{{PA}}{{OP}}$
And
$\Rightarrow \beta = \dfrac{{PA}}{{IP}}$
Also
$\Rightarrow \gamma = \dfrac{{PA}}{{CP}}$
Substituting these values of $\alpha ,\beta$ and $\gamma$ in , we get
$\Rightarrow \dfrac{{PA}}{{PC}} - \dfrac{{PA}}{{PO}} = \mu \left( {\dfrac{{PA}}{{PC}} - \dfrac{{PA}}{{PI}}} \right)$
Taking the common terms outside we get,
$\Rightarrow PA\left( {\dfrac{1}{{PC}} - \dfrac{1}{{PO}}} \right) = \mu PA\left( {\dfrac{1}{{PC}} - \dfrac{1}{{PO}}} \right)$
$\Rightarrow PA$ gets cancelled as it is common on both sides. Now we have
$\Rightarrow \dfrac{1}{{PC}} - \dfrac{1}{{PO}} = \mu \left( {\dfrac{1}{{PC}} - \dfrac{1}{{PI}}} \right)$
Now we have to apply the sign convention.
$\Rightarrow PC = - R$ (where $R$ is the radius of curvature)
$\Rightarrow PI = - v$ (Where $v$ is the distance of the image from the pole of the mirror)
$\Rightarrow PO = - u$ (Where $u$ is the distance of the object from the pole of the mirror)
Putting these values in equation
We get,
$\Rightarrow \left( {\dfrac{1}{{ - R}}} \right) - \left( {\dfrac{1}{{ - u}}} \right) = \mu \left( {\dfrac{1}{{ - R}} + \dfrac{1}{v}} \right)$
Opening the brackets on LHS
$\Rightarrow\dfrac{{ - 1}}{R} + \dfrac{1}{u} = \mu \left( {\dfrac{{ - 1}}{R} + \dfrac{1}{v}} \right)$
Opening the brackets on RHS
$\Rightarrow \dfrac{{ - 1}}{R} + \dfrac{1}{u} = \dfrac{\mu }{R} + \dfrac{\mu }{v}$
Rearranging, we get
$\Rightarrow \dfrac{{ - 1}}{R} + \dfrac{\mu }{R} = \dfrac{\mu }{v} - \dfrac{1}{u}$
We can write this expression as,
$\Rightarrow \dfrac{{\mu - 1}}{R} = \dfrac{\mu }{v} - \dfrac{1}{u}$
Hence we got the required expression for the concave refractive surface.

Note
According to the Cartesian sign convention,
-All distances as measured from the pole of the mirror.
-The distances that are measured in the direction of the incident light are taken as positive.
-The distances that are measured opposite to the direction of incident light is considered as negative.
-The height measured upward the principal axis is measured as positive and the height measured downward is measured negative.