Question

Derive the expression for the potential energy of a system of two charges in the absence of the external electric field.

Answer 1

The potential energy of this system of charge is equal to total work done ,i.e., To move charge q$_{1}$ from infinity to A and charge q$_{2}$ from infinity to B. when we bring charge q$_{2}$ from infinity to point B, q$_{1}$ is also taken into account, whereas in case of q$_{1}$, the charge q$_{2}$ is not taken because there is no initial electric field.

Complete step-by-step answer:
__

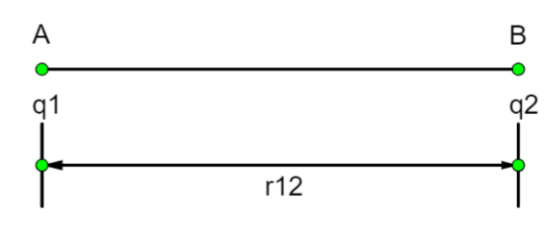
The work done to move q from infinity to A is, $W_1$
($\therefore$ There is no initial electric field hence work done to bring charge q$_{1}$ from infinity to A is zero)
The work done to move q$_{2}$ from infinity to B is, ${W_1} = {V_1}{q_1}$
Here,${V_1}$ is the electric potential at B due to ${q_1}$ , it is given by:
${V_1} = \dfrac{1}{{4\pi {\xi _ \circ }}}\left( {\dfrac{{{q_1}}}{{{r_{12}}}}} \right)$
$\Rightarrow {W_2} = {V_1}{q_2} = {V_1} = \dfrac{1}{{4\pi {\xi _ \circ }}}\left( {\dfrac{{{q_1}}}{{{r_{12}}}}} \right){q_2}$
${W_2} = \dfrac{1}{{4\pi {\xi _ \circ }}}\left( {\dfrac{{{q_1}{q_2}}}{{{r_{12}}}}} \right)$
The potential energy of this system of charge is equal to total work done to bring the charges from infinity to A or B.
$U = {W_1} + {W_2} = 0 + \dfrac{1}{{4\pi {\xi _ \circ }}}\left( {\dfrac{{{q_1}{q_2}}}{{{r_{12}}}}} \right)$
$U = \left( {\dfrac{1}{{4\pi {\xi _ \circ }}}} \right)\left( {\dfrac{{{q_1}{q_2}}}{{r{}_{12}}}} \right)$
$U = K\left( {\dfrac{{{q_1}{q_2}}}{{{r_{12}}}}} \right)$. (Where,$K = \left( {\dfrac{1}{{4\pi {\xi _ \circ }}}} \right)$ )

Note: Generally students can go wrong in considering the work done to move charge q$_{1}$ from infinity to A where there is no external electric field working, the same goes for charge q$_{2}$ where actually the charge q$_{1}$ affects the work done. We can also consider q$_{2}$ as the first charge which comes into the system from infinity in that case q$_{1}$ will not affect the work done to bring the charge from infinity to B, but q$_{2}$ will affect work done to bring charge $q_{1}$ to A.