Question

Derive the expression for the fringe width in Young's double-slit experiment. How will the fringe width change if
(A) The separation between the slits is increased
(B) The screen moved away from the plane of the slits.

Answer 1

Hint
The interference between two coherent rays is studied in Young's double-slit experiment. When two coherent rays interfere they will produce a pattern of alternate bright and dark fringes. In Young's double-slit experiment we have two slits separated by a distance that acts as a coherent source. The pattern is obtained using a screen placed at a distance.

Complete step by step answer

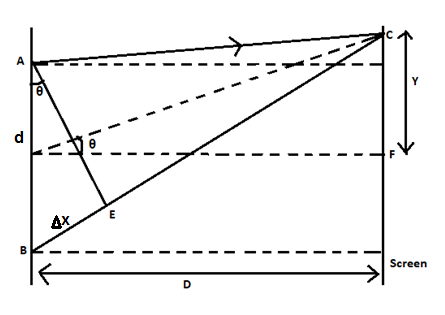
In the figure, A and B represent the two slits through which the light passes. A screen is placed at a distance $D$ . When monochromatic light passes through the slits, the spherical wavefronts will interfere. As a result, we will get a pattern on the screen.
We know that there is a difference in the paths traveled by the two rays of light $AC$ and $BC$ . This difference in the path traveled by the rays is called the path difference and it can be obtained by considering the two triangles $\Delta ABE$ and $\Delta ACE$ .
Here the path difference is given by, $BE = AB\sin \theta$ $\left( {\because \sin \theta = \dfrac{{BE}}{{AB}}} \right)$
We know that $AB$ is the distance between the two slits and it can be taken as $d$ .
Let us denote the path difference as $\Delta x$
Now we can write the path difference as,
$\Rightarrow \Delta x = d\sin \theta$ … equation
For small values of $\theta$ we can write $\sin \theta \approx \tan \theta$
From the figure we can write, $\sin \theta \approx \tan \theta = \dfrac{Y}{D}$
Substituting in the equation, we get
$\Rightarrow \Delta x = d\left( {\dfrac{Y}{D}} \right)$
$\Rightarrow \dfrac{{\Delta x}}{d} = \dfrac{Y}{D}$
We assume that $Y$ is the distance between the centre of the screen and the point where the fringe is formed.
Then,
$\Rightarrow Y = \dfrac{{\Delta xD}}{d}$
The separation between two consecutive dark fringes or bright fringes is called the fringe width.
We can write the path difference as, $\Delta x = n\lambda$
Where $n$ is an integer called the order of the fringe and $\lambda$ is the wavelength of the monochromatic source of light.
Now we can find the separation between two fringes using the expression
$\Rightarrow Y = \dfrac{{n\lambda D}}{d}$
For an ${n^{th}}$ order fringe, ${Y_n} = \dfrac{{n\lambda D}}{d}$
And the ${\left( {n + 1} \right)^{th}}$ order fringe, ${Y_{n + 1}} = \dfrac{{(n + 1)\lambda D}}{d}$
Let $\beta$ be the separation between two consecutive bright or dark fringe then
The fringe width can be written as,
$\Rightarrow \beta = \dfrac{{\left( {n + 1} \right)\lambda D}}{d} - \dfrac{{n\lambda D}}{d}$
$\Rightarrow \dfrac{{\lambda D}}{d}\left( {n + 1 - n} \right)$
Therefore we get,
$\Rightarrow \beta = \dfrac{{D\lambda }}{d}$
Now we get that
- The width of the fringes is inversely proportional to the separation between the slits, i.e. when the separation between the slits $\left( d \right)$ increases, the fringe width will decrease.
- The separation between the slits and the screen is directly proportional to the fringe width i.e. when the separation between the slits and the screen $\left( D \right)$ increases the fringe width increases.

Note
The fringe width is independent of the order of the fringe. We can also see from the expression that it is directly proportional to the wavelength of the source. That is the fringes produced for red light will be wider than the fringes produced by blue light. Interference will occur only when the light from two different sources will have the same frequency.