Question
Question: Derive the expression for the electric potential at any point along the axial line of an electric di...
Derive the expression for the electric potential at any point along the axial line of an electric dipole?
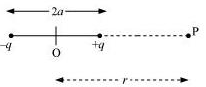
Solution
An electric potential is defined as the amount of work required to move a unit of electric charge from a reference to a specific point in an electric field without producing acceleration. The electric potential at a given point for a group of charges will be equal to the algebraic sum of the potentials due to individual charges. An electric dipole is an arrangement of two equal and opposite charges that are separated by a finite distance. Its units are coulomb-meter.
Let P be the axial point at a distance r from the center of the dipole. The Electric potential at point P is given as
V = V1+V2
Let V1 and V2 are the potentials at point P due to the charges +q and −q respectively.
∴ Then the Electric Potential, V = 4πεo1((r−2aq)+(r+2a−q)) (∵V=4πεo1rq)
Here ε0 is the permittivity of the vacuum, q is the charge and r is the distance
⇒V = 4πεo1((r2−4a2)4aq)
⇒V = 4πεo1((r2−4a2)2P) (∵qa=P/2)
∴ The expression for the electric potential is V = 4πεo1(r2−4a22P)
Note: 1) The electric potential for a system of point charges will be equal to the sum of the point charges of the individual potentials.
2) The electric potential is a scalar quantity and has no direction. It is also called the electric field potential or electrostatic potential or potential drop.
3) Electric potential can also be defined as potential energy per unit charge.
4) The potential at an infinite distance is often taken to be zero.
5) Dipoles are mostly found in the molecular structures which are caused by the non-uniform charge distribution of protons and electrons.
