Question

Derive the expression for the angular magnification of a simple microscope.

Answer 1

Hint : When the object is at a distance closer than the distance of the least distinct vision, we can use a microscope to view the object clearly. The angular magnification of a microscope is defined as the ratio of the angle subtended by the image after refraction from the microscope to the angle subtended by the object at an unaided eye/without the apparatus.

Complete step by step answer
The angular magnification is defined as follows:
${\text{M = }}\dfrac{{{\text{angle subtended by eye using instrument}}}}{{{\text{angle subtended at unaided eye}}}}$

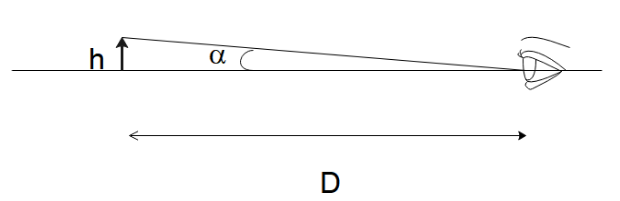
When looking at a small object, as shown above, the angle subtended by the object at the unaided eye is very small and can be approximately written as
$\alpha = \dfrac{h}{d}$

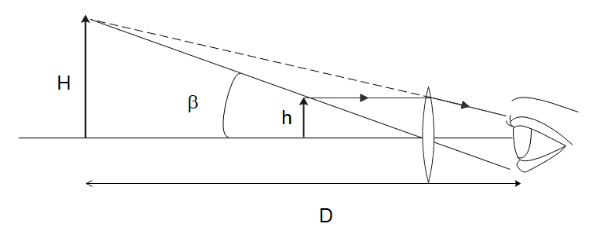
When a lens is placed in between the object and the eye as is done in a simple microscope shown above, the angle subtended by the object will be
$\beta = \dfrac{H}{d}$
Since the image will be formed at the least distance of distinct vision $D$, i.e. $d = D$, the angular magnification can be defined as:
$M = \dfrac{\alpha }{\beta } = \dfrac{{H/D}}{{h/D}}$
$\Rightarrow M = \dfrac{H}{h}$
Now from the lens-maker formula, we can write
$\dfrac{1}{v} - \dfrac{1}{u} = \dfrac{1}{f}$
We can rearrange the above equation to write,
$\dfrac{v}{f} = 1 + \dfrac{v}{u}$
Since the ratio of the image to the object position is also equal to magnification and we want the image to form at the least distance of distinct vision $D$ which is typically $25\,cm$, we can say $v/u = M$ and $v = D$ and hence write
$M = \dfrac{D}{f} - 1$
This is the magnification power for a simple microscope to form an image at the least distance of distinct vision of the observer.

Note
If the object is placed at infinity, the angle $\beta$ subtended by the object is the same with or without the lens as. Also, the image formed by the lens will be formed at a distance equal to the focal length of the lens. So $d = f$ and we can write
$\beta = \dfrac{h}{f}$
So,
$M = \dfrac{\alpha }{\beta } = \dfrac{{h/f}}{{h/D}}$
$\Rightarrow M = \dfrac{D}{f}$