Question
Question: Derive the expression for refractive index of the material of the prism in terms of angle of the pri...
Derive the expression for refractive index of the material of the prism in terms of angle of the prism and angle of minimum deviation.
Solution
Hint: First draw a ray diagram indicating a ray of incidence and a ray of emergence. Then indicate all the necessary angles in the diagram. Then by using the conditions of minimum deviation derive an expression for the angle of incidence and angle of refraction. And the last stage would be the application of Snell’s law to get to the answer.
Formula used:
Snell’s law states that when a light wave passes through the interface of two different media, the ratio of sine of angle of incidence and refraction is a constant.
Mathematically, μ=sinrsini
Complete step-by-step answer:
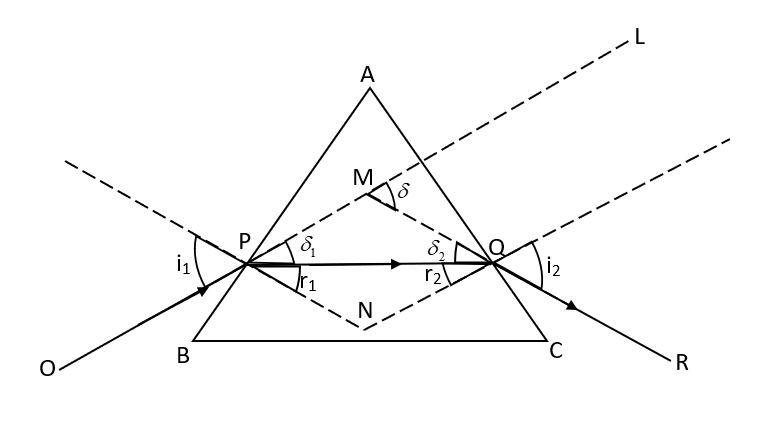
Let us consider a ray diagram for a prism in which OP is the ray of incidence which makes angle i1 with the normal at side AB and i2 is the angle of emergence with the normal at side AC. ∠A is the prism angle and let μ be the refractive index of the prism. δ be the angle of deviation
According to the question, minimum deviation is taking place and we know that for minimum deviation, r1=r2=r, i1=i2=i and δ=δm.
And we know that ∠A=r1+r2
∴∠A=r+r=2r
And, r=2A
Also, A+δ=i1+i2⟹A+δm=i+i⟹i=2A+δm
Now, from Snell’s law, we can write that μ=sinrsini
⟹μ=sin2Asin2A+δm
This is the expression for refractive index.
Note: The conditions of minimum deviation are required in this question and should be applied correctly. Snell’s law for light waves passing through an interface of two media is also a key concept in determining the expression for the refractive index. An assumption has also been made here that the refractive index of the surrounding medium is 1.
