Question

Derive the expression for energy stored in a charged capacitor.

Answer 1

The relation between Capacitance, charge and electrical potential. The work done to accumulate charge in a capacitor is the energy stored in a capacitor. Relation between electrical potential and work done.

Formula used: $V=\dfrac{Q}{C}$, where, V represents the electrical potential, C represents the capacitance and Q represents the charge stored in a capacitor.
The work done to move a test charge $dQ$ is given by the expression $dW=VdQ$
Also, $\int_{a}^{b}{{{x}^{n}}dx}=\dfrac{{{b}^{n+1}}-{{a}^{n+1}}}{n+1}$

Complete step by step answer:

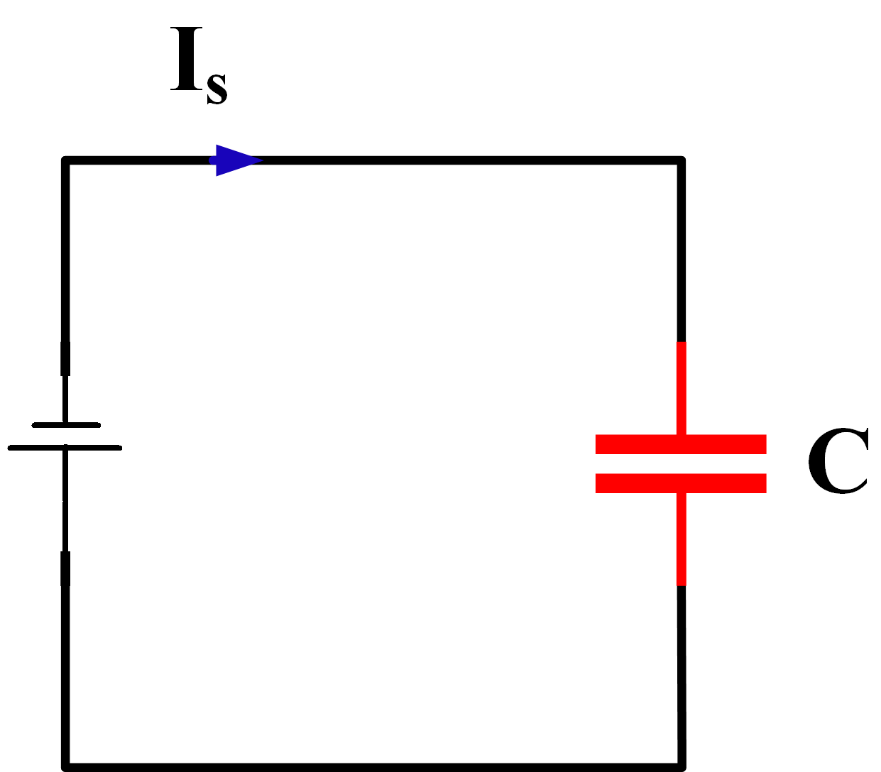
A capacitive circuit is shown in the above figure. In a circuit, with voltage around the capacitor V, the Capacitance C is given by the equation:
$Q=CV$…(1)
Where, Q represents the charge stored in the capacitor.
Now, we want to find the energy stored in a capacitor.
According to electrostatics, the energy stored in a capacitor will be equal to the work done to move the charge into the capacitor having an electrical potential V.
Or
$dW=VdQ$…(2)
Now, for a capacitor, $V=\dfrac{Q}{C}$…(3)
So, we can put the value of V from equation (3) into equation (2).
This gives,
$dW=\dfrac{Q}{C}dQ$,
Now the total work done to move charge Q can be found by integration,
$\int_{0}^{W}{dW}=\dfrac{1}{C}\int_{0}^{Q}{QdQ}$
Now, from the integration method given in the formula used section, we can calculate the following result.
$W=\dfrac{1}{2}\dfrac{{{Q}^{2}}}{C}$, This is also equal to the energy stored in the capacitor.
Therefore, $U=\dfrac{1}{2}\dfrac{{{Q}^{2}}}{C}$
Moreover, from equation (1), we can put ${{Q}^{2}}={{\left( CV \right)}^{2}}$
This will give us,
$U = \dfrac{1}{2}\dfrac{{{Q^2}}}{C} = \dfrac{1}{2}C{V^2}$

Additional Information: A capacitor is a device in which equal and opposite charges are separated by a distance in space.
The capacitor shown in the books is usually a parallel plate capacitor.
Cylindrical capacitors are used in many electrical devices.
The SI unit is farad. It is defined as the capacitance which stores 1 C of charge along 1 V potential difference,

Note: The value of capacitance in a parallel plate is given by $C=\varepsilon \dfrac{A}{d}$, where, $\varepsilon$is the permittivity of medium between the plates, A is the area of the plates and d is the distance between the plates. The question can also be solved by substituting the value of $C=\varepsilon \dfrac{A}{d}$, in equation (3). This will give an answer in terms of area and distance of the plates.