Question

Derive the equation of motion using the calculus method?

Answer 1

In this question, we need to derive the equations of motion strictly by using calculus only. The instantaneous acceleration of a moving particle is defined as the rate of change of velocity of the particle. The equations of motion describe the behavior of a physical system as a set of mathematical functions in terms of dynamic variables.

Complete step by step answer:
Let us consider a particle is moving in a straight line with uniform acceleration$'a'$. The initial velocity of the particle is $u$ , and after time $'t'$the final velocity becomes$'v'$. Let’s say the particle is moving from A to B, where $AB = s$, i.e., $s$is the displacement of the particle.
The first equation of motion is $\left[ {v = u + at} \right]$:
The rate of change of velocity of a particle is known as the acceleration of the particle, i.e., $\Rightarrow a = \dfrac{{dv}}{{dt}}$. This equation can also be written as:
$\Rightarrow a = \dfrac{{dv}}{{dt}} \\\ \Rightarrow dv = adt \\\$
Integrating both sides of the above equation, we get
$\Rightarrow \int {dv = \int {adt} }$

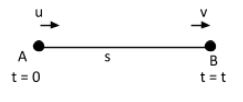
For applying the limit of integration we choose,
(I) when the particle was at $A(t = 0),$the velocity of the particle was $u$ , and it becomes $v$ at the time $B\left( {t = t} \right)$,

\Rightarrow\int\limits_u^v {dv} = \int\limits_0^t {adt} \\\ \Rightarrow\int\limits_u^v {dv} = a\int\limits_0^t {dt} \\\ \Rightarrow \left[ v \right]\begin{array}{*{20}{c}} v \\\ u \end{array} = a\left[ t \right]\begin{array}{*{20}{c}} t \\\ o \end{array} \\\ \Rightarrow v - u = a\left( {t - 0} \right) \\\ \Rightarrow v - u = at \\\ \Rightarrow v = u + at \\\

The second equation of motion is $\left[ {s = ut + \dfrac{1}{2}a{t^2}} \right]$:
We know the acceleration in the form of displacement is given by, $a = v\left( {\dfrac{{dv}}{{ds}}} \right)$
The equation can also be written as:
$\Rightarrow ads = vdv........\left( i \right)$
From the first equation of motion, i.e.,$v = u + at$
Differentiating this equation with respect to time, we will get
$\Rightarrow \dfrac{{dv}}{{dt}} = 0 + a \\\ \Rightarrow \dfrac{{dv}}{{dt}} = a \\\ \Rightarrow dv = adt \\\$
Putting these values $\left( {v = u + at} \right)$and $\left( {dv = a\,\,dt} \right)$in equation (i), we have
$\Rightarrow ads = \left( {u + at} \right)\left( {adt} \right) \\\ \Rightarrow ds = \left( {u + at} \right)dt \\\$
Integrating both sides:
\Rightarrow \int\limits_0^s {ds} = \int\limits_0^t {\left( {u + at} \right)} dt \\\ \Rightarrow \int\limits_0^s {ds = \int\limits_0^t {udt + a\int\limits_0^t {tdt} } } \\\ \Rightarrow\left[ s \right]\begin{array}{*{20}{c}} s \\\ 0 \end{array} = u\left[ t \right]\begin{array}{*{20}{c}} t \\\ 0 \end{array} + a\left[ {\dfrac{{{t^2}}}{2}} \right]\begin{array}{*{20}{c}} t \\\ 0 \end{array} \\\ \Rightarrow s - 0 = u\left( {t - 0} \right) + \dfrac{a}{2}\left( {{t^2} - {0^2}} \right) \\\ \Rightarrow s = u + \dfrac{1}{2}a{t^2} \\\
The third equation of motion is $\left[ {{v^2} = {u^2} + 2us} \right]$:
From equation (i), we can write
$ads = vdv$
Integrating both sides, we get
\Rightarrow a\int\limits_0^s {ds} = \int\limits_u^v {udv} \\\ \Rightarrow a\left[ s \right]\begin{array}{*{20}{c}} s \\\ 0 \end{array} = \left[ {\dfrac{{{v^2}}}{2}} \right]\begin{array}{*{20}{c}} v \\\ u \end{array} \\\ \Rightarrow a\left( {s - 0} \right) = \dfrac{1}{2}\left( {{v^2} - {u^2}} \right) \\\ \Rightarrow as = \dfrac{1}{2}\left( {{v^2} - {u^2}} \right) \\\ \Rightarrow 2as = \left( {{v^2} - {u^2}} \right) \\\ \Rightarrow {v^2} = {u^2} + 2as \\\

Note: The motion of equations are valid for a uniform acceleration. If the acceleration of the particle is not uniform, then we use integration for calculating the value of acceleration. The formula for the acceleration of the particle is
(i) $a = \dfrac{{dv}}{{dt}}$
(ii) $a = v\left( {\dfrac{{dv}}{{ds}}} \right)$.
The equations of motion are equations that describe the behavior of a physical system in terms of its motion as a function of time.