Question

Derive the equation of motion of bodies connected by string (Atwood’s machine).

Answer 1

To solve this question, we have to employ the use of a free-body diagram. The free-body diagram can be used to calculate the forces acting on the masses. From the force, we can calculate the acceleration of the bodies which represents the equation of motion of the bodies.

Complete solution:
The Atwood’s machine consists of two masses hanging on either sides of a smooth frictionless pulley and connected by a light massless string. The representation of the Atwood’s machine is shown here:

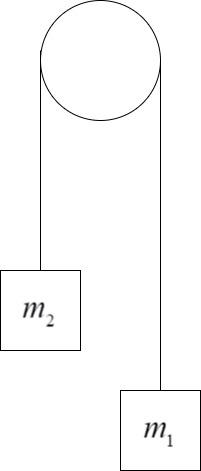
Here, we have to assume that the mass ${m_1} > {m_2}$. This means that the acceleration of the mass ${m_1}$ will be in downward direction thereby, pulling the other mass ${m_2}$ in the other direction, upwards.
The acceleration can be calculated by the free-body diagrams of the individual masses. Free-body diagram of ${m_2}$ mass:

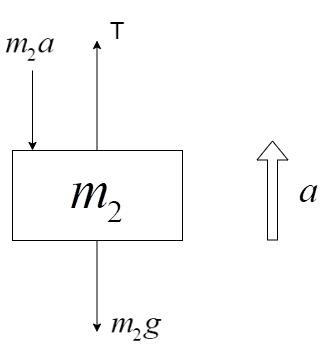
The acceleration is pointed upwards since the mass ${m_1}$ is heavier and it pulls the ${m_2}$ mass in the upward direction over the pulley.
The forces acting on the ${m_2}$ mass are:
i) Weight, ${m_2}g$
ii) Tension due to the string, T
iii) Force acting due to the acceleration a, in the direction opposite of the acceleration and equal to ${m_2}a$.
Equating the forces, we get –
${m_2}a + {m_2}g = T \Rightarrow \left( 1 \right)$
Free-body diagram of ${m_1}$ mass:

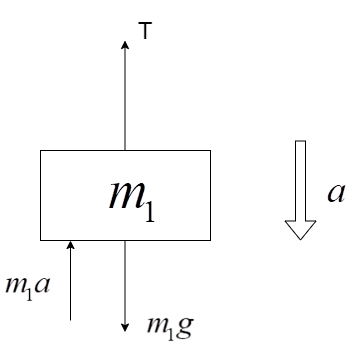
The acceleration is pointed downwards since the mass ${m_1}$ is heavier and it pulls the ${m_2}$ mass in the upward direction over the pulley.
The forces acting on the ${m_1}$ mass are:
i) Weight, ${m_1}g$
ii) Tension due to the string, T
iii) Force acting due to the acceleration a, in the direction opposite of the acceleration and equal to ${m_1}a$.
Equating the forces, we get –
$T + {m_1}a = {m_1}g$
${m_1}g - {m_1}a = T \Rightarrow \left( 2 \right)$
Equating $\left( 1 \right)$ and $\left( 2 \right)$, we get –
${m_2}a + {m_2}g = {m_1}g - {m_1}a$
$\Rightarrow {m_1}a + {m_2}a = {m_1}g - {m_2}g$
$\Rightarrow a\left( {{m_1} + {m_2}} \right) = g\left( {{m_1} - {m_2}} \right)$
$\therefore a = g\left( {\dfrac{{{m_1} - {m_2}}}{{{m_1} + {m_2}}}} \right)$

Thus, the equation of motion for the system of bodies is –
Acceleration of the system, $a = g\left( {\dfrac{{{m_1} - {m_2}}}{{{m_1} + {m_2}}}} \right)$.

Note: The acceleration of the system is very important parameter to assess the motion since the acceleration can be used to easily calculate the final velocity in a given duration of time or by a given displacement through the following formulae –
$v = u + at$
${v^2} - {u^2} = 2as$
where u = initial velocity, v = final velocity, a = acceleration, t = time taken and s = displacement.