Solveeit Logo
Login

Question

Question: Derive mirror equation. State any three experimental observations of photoelectric emission....

Derive mirror equation. State any three experimental observations of photoelectric emission.

Explanation

Solution

In a spherical mirror, the distance of the object from its pole is called the object distance (u). The distance of the image from the pole of the mirror is called the image distance (v). The distance of the principal focus from the pole is called the focal length (f). There is a relationship between these three quantities given by the mirror formula which is expressed as 1v+1u=1f\dfrac{1}{v} + \dfrac{1}{u} = \dfrac{1}{f}.This formula is valid in all situations for all spherical mirrors for all positions of the object.

Complete step by step solution:
Derivation of the Mirror Formula

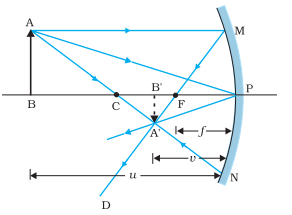
We now derive the mirror equation or the relation between the object distance (u), image distance (v) and the focal length (f). In the above figure, the two right-angled triangles A′B′F and MPF are similar.
⇒B′A′PM=B′FFP ⇒B′A′BA=B′FFP ∵PM=AB...............(1) ⇒∠APB=∠A′PB ∴ΔA′B′P′∼ΔAB′P ∴B′A′BA=B′PBP............(2) By comparing equation(1) and (2), we get ⇒B′FFP=B′P−FPFP=B′PBP ⇒B′P=−v,FP=−f,BP=−u Usin⁡g these in equation, we get ⇒−v+f−f=−v−u ⇒v−ff=vu On further solving, we get ∴1v+1u=1f  \Rightarrow \dfrac{{{B'}{A'}}}{{PM}} = \dfrac{{{B'}F}}{{FP}} \\\ \Rightarrow \dfrac{{{B'}{A'}}}{{BA}} = \dfrac{{{B'}F}}{{FP}} \\\ \because PM = AB...............(1) \\\ \Rightarrow \angle APB = \angle {A'}PB \\\ \therefore \Delta {A'}{B'}{P'} \sim \Delta A{B'}P \\\ \therefore \dfrac{{{B'}{A'}}}{{BA}} = \dfrac{{{B'}P}}{{BP}}............(2) \\\ By{\text{ }}comparing{\text{ }}equation(1){\text{ }}and{\text{ }}(2),{\text{ }}we{\text{ }}get \\\ \Rightarrow \dfrac{{{B'}F}}{{FP}} = \dfrac{{{B'}P - FP}}{{FP}} = \dfrac{{{B'}P}}{{BP}} \\\ \Rightarrow {B'}P = - v,FP = - f,BP = - u \\\ U\sin g{\text{ }}these{\text{ }}in{\text{ }}equation,{\text{ }}we{\text{ }}get \\\ \Rightarrow \dfrac{{ - v + f}}{{ - f}} = \dfrac{{ - v}}{{ - u}} \\\ \Rightarrow \dfrac{{v - f}}{f} = \dfrac{v}{u} \\\ On{\text{ }}further{\text{ }}solving,{\text{ }}we{\text{ }}get \\\ \therefore \dfrac{1}{v} + \dfrac{1}{u} = \dfrac{1}{f} \\\
Note: In a spherical mirror, the distance of the object from its pole is called the object distance (u). The distance of the image from the pole of the mirror is called the image distance (v). The distance of the principal focus from the pole is called the focal length (f). There is a relationship between these three quantities given by the mirror formula which is expressed as 1v+1u=1f\dfrac{1}{v} + \dfrac{1}{u} = \dfrac{1}{f}.This formula is valid in all situations for all spherical mirrors for all positions of the object.