Question

Derive mathematical expression for first law of thermodynamics?

Answer 1

From thermodynamics first law, the total energy associated with a system is constant, but its form can be changed. In other words, we can say that the work done by a system in a cyclic process is equal to the heat supplied to it.

Complete step by step answer:
Let us consider a system undergoing a process from state first to state second by following the path ‘a’ and returns from state second to state first by following path ‘b’ and path ‘c’ as shown below.

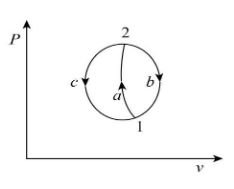
From the concept of the first law of thermodynamics, for the cyclic process 1-a-2-b-1 we can write:
$\oint_{1 - a - 2 - b - 1} {\left( {Q - W} \right)} = 0$
We can break the above cyclic process into two processes 1-a-2 and 2-b-1, that is,
$\int_{1 - a - 2} {\left( {Q - W} \right)} + \int_{2 - b - 1} {\left( {Q - W} \right)} = 0$……(1)
Process 1-a-2-c-1 is also a cyclic process so that we can write:
$\oint_{1 - a - 2 - c - 1} {\left( {Q - W} \right)} = 0$
We can break the above cyclic process into process 1-a-2 and process 2-c-1.
$\int_{1 - a - 2} {\left( {Q - W} \right)} + \int_{2 - c - 1} {\left( {Q - W} \right)} = 0$……(2)
On comparing the equation (1) and equation (2), we can write:
$\int_{2 - b - 1} {\left( {Q - W} \right)} = \int_{2 - c - 1} {\left( {Q - W} \right)}$
By closely observing equation (1) and equation (2) we can conclude that the value of the above expression is non-zero.

\int_{2 - b - 1} {\left( {Q - W} \right)} = \int_{2 - c - 1} {\left( {Q - W} \right)} \\\ \ne 0 \end{array}$$ Based on the above expression, we can say that the term $$\int_{2 - b - 1} {\left( {Q - W} \right)} $$ and term $$\int_{2 - c - 1} {\left( {Q - W} \right)} $$ have some value which is independent of path. Hence, it is a point function. We know that point functions are properties of a thermodynamic system which is an exact differential, and this non-zero term is defined as the energy of the system. $$\begin{array}{l} \int_{2 - b - 1} {\left( {Q - W} \right)} = \int_{2 - c - 1} {\left( {Q - W} \right)} \\\= dE \end{array}$$ By generalising the above expression for a non-cyclic process, we can write: $$\begin{array}{l} Q - W = dE\\\ Q = W + dE \end{array}$$ Therefore, the mathematical relationship of the first law of thermodynamics for a non-cyclic process is $$Q = W + dE$$. **Note:** In this problem, we can note that the state of a system is a point function, hence exact differential. We know that exact differential are properties of the system that’s why we defined a point function as the property of the system.