Question
Question: Derive lens maker’s formula for a convex lens....
Derive lens maker’s formula for a convex lens.
Solution
Making a neat ray diagram of the image formation by a convex lens prior to derivation is an unavoidable step. Then, you could apply the formula that we use for the case of refraction on spherical surfaces for the two spherical surfaces of the lens. Thereby, you will be able to derive the required formula with necessary rearrangements and substitutions.
Formula used:
For spherical refracting surfaces, we have,
vn2−un1=Rn2−n1
Complete Step by step solution:
In the question, we are asked to derive the lens maker’s formula for a convex lens. For that let us consider a convex lens.
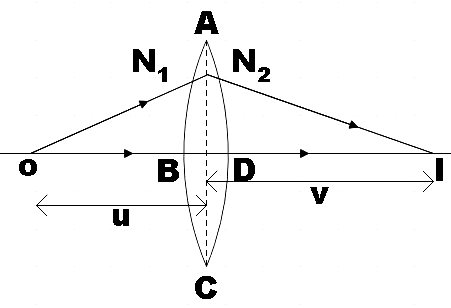
This is how the geometry of the image formation by a double convex lens would look like. The image formation actually takes place in two steps: the first refracting surface forms the image I1 of the object O. This image then becomes the virtual object for the second surface that forms the image I.
For the first spherical surface,
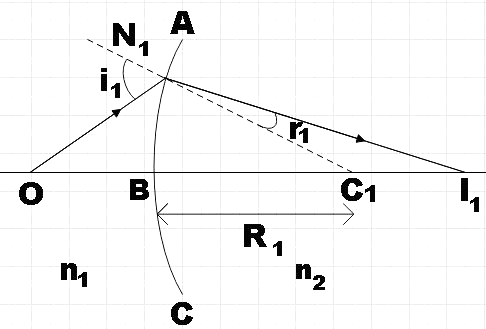
We know that the refraction at a spherical surface is given by,
vn2−un1=Rn2−n1 …………………………………………… (1)
⇒OBn1+BI1n2=BC1n2−n1 ………………………………………. (2)
Now, for the second spherical surface,
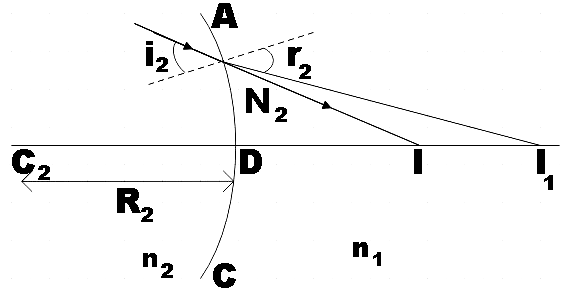
−DI1n2+DIn1=DC2n2−n1 ………………………………………. (3)
For a very thin lens, we could say that,
BI1=DI1
Now on adding (2) and (3) we get,
OBn1+DIn1=(n2−n1)(BC11+DC21)
If the object was kept at infinity, the image would be formed at the focal point, that is,
IfOB=∞, then, DI=f
⇒fn1=(n2−n1)(BC11+DC21)
From the given figure, we see that BC1 and DC2 are the radius of curvatures of the two spherical surfaces. Also, by convention,
BC1=+R1
DC2=−R2
⇒f1=(n21−1)(R11−R21)
Where, n21=n1n2
Thereby, we have derived the lens maker’s formula which is used for designing lenses of desired focal length using spherical surfaces of suitable radii of curvature.
Note:
As per convention we take measurements with respect to the optical axis. The measurements made to the right side of it are taken positive and that to the left side are taken negative. Also, the lens maker’s formula that we derived is also true for concave lenses. But, remember the sign convention while substituting the radii of curvature.
