Question

Derive an expression of the magnetic field at the center of a circular current carrying coil.

Answer 1

Hint: A wire carrying current has a magnetic field. The intensity of the magnetic field at any point is obtained by the Biot-Savart’s law.
This law in vector form can be written as
$d\vec B = \dfrac{{{\mu _0}}}{{4\pi }}i\dfrac{{d\vec l \times \hat r}}{{{r^2}}}$

Step by step solution:

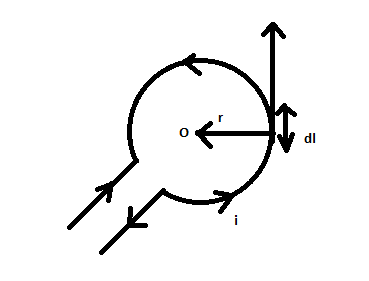
1. Consider a current carrying circular loop having its center at O carrying current i. If dl is a small element at a distance r then, the magnetic field intensity on that point can be written using Biot-Savart’s law.

$$d\vec B = \dfrac{{{\mu _0}}}{{4\pi }}i\dfrac{{d\vec l \times \hat r}}{{{r^2}}} \\\ \left| {d\vec B} \right| = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{idl\sin \theta }}{{{r^2}}} \\\$$

2. As the loop is circular then,
   $\theta = {90^ \circ }$
   $\sin \theta = 1$
3. Putting this in the Biot-Savart’s law we will get,
   $\left| {d\vec B} \right| = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{idl}}{{{r^2}}}$
4. If we think that the circular loop is composed of numbers of such small element dl, then we will get the magnetic intensity for all over the loop. So to get the total field we must sum up that is integrate the magnetic field all over the field.

$$B = \int\limits_0^B {d\vec B} \\\ B = \int {\dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{idl}}{{{r^2}}}} \\\ B = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{i}{{{r^2}}}\int {dl} \\\$$

5. As the integration over dl returns the circumference of the loop then, you can write,

$$\int {dl} = 2\pi r \\\ B = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{i}{{{r^2}}}2\pi r \\\ B = \dfrac{{{\mu _0}i}}{{2r}} \\\$$

Hence the magnetic field at the center of the circular coil is $B = \dfrac{{{\mu _0}i}}{{2r}}$.

Note: Field due to a semi-circular coil is just half that of the circular coil.
$B = \dfrac{{{\mu _0}i}}{{4r}}$