Question

Derive an expression of magnetic field due to long current carrying solenoid?

Answer 1

1. Solenoid: It is a cylindrical coil made of wire acting as a magnet when current flows through it.
2. Solenoid behaves as an electromagnet.
3. Solenoid is coated with an iron core that increases the magnetic effect of the coil.
4. The magnetic effect in the solenoid is used to produce a straight line in motion.
5. Solenoid is designed to convert electrical energy into mechanical energy.
6. When current is allowed to cross inside the solenoid coil magnetic field is produced around the solenoid coil.

Complete step by step solution:
Consider a solenoid of the radius $\left( a \right)$, having the length $\left( {2L} \right)$, and $\left( n \right)$ be the number of the turns in the solenoid per unit length. The magnitude of the current flowing in the solenoid is $\left( I \right)$.
Consider a circular elemental section of the thickness $\left( {dx} \right)$ which is at a distance of $\left( x \right)$ from the center.

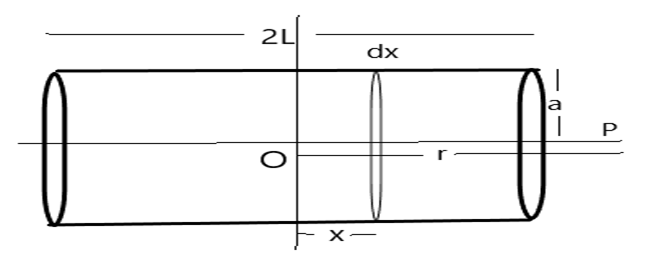
The elementary magnetic field produced in the $\left( {dx} \right)$ region is ${\text{dB = }}\dfrac{{{\mu _0}{\text{dxnI}}{{\text{a}}^2}}}{{2{{[{{({\text{r - x)}}}^2} + {{\text{a}}^2}]}^{\dfrac{3}{2}}}}}$
Integrating the term, we will get the magnetic field for the $\left( {2L} \right)$ length of the solenoid,
We note that here the value of $\left( x \right)$ is varying from $- L$ to $+ L$.
Therefore, we get that$\int {{\text{dB = }}\dfrac{{{\mu _0}{\text{nI}}{{\text{a}}^2}}}{2}\int\limits_{ - {\text{L}}}^{ + {\text{L}}} {\dfrac{{{\text{dx}}}}{{2{{[{{({\text{r - x)}}}^2} + {{\text{a}}^2}]}^{\dfrac{3}{2}}}}}}}.$
Considering the axial field is far from the center of the solenoid, $r > > a$,
Therefore, we can write that, $[{({\text{r - x)}}^2} + {{\text{a}}^2}] \approx {{\text{r}}^2}$
Now, substituting the value in the equation we get that,
${\text{B = }}\dfrac{{{\mu _0}{\text{nI}}{{\text{a}}^2}}}{{2{{\left( {{{\text{r}}^2}} \right)}^{\dfrac{3}{2}}}}}\int\limits_{ - {\text{L}}}^{{\text{ + L}}} {{\text{dx}}}$
On integral we get,
$\Rightarrow \dfrac{{{\mu _0}{\text{nI}}{{\text{a}}^2}}}{{2{{\text{r}}^3}}}2{\text{L}}$
On cancelling the term and we get,
$B = \dfrac{{{\mu _0}{\text{nI}}{{\text{a}}^2}}}{{{{\text{r}}^3}}}$

Hence, the required expression for the magnetic field in the solenoid is $\dfrac{{{\mu _0}{\text{nI}}{{\text{a}}^2}}}{{{{\text{r}}^3}}}.$

Note:
1. Magnetic field lines never cross each other.
2. All the magnetic field lines have the same strength around the solenoid.
3. The density of the magnetic field decreases with the increase of the distance from the pole.
4. Magnetic field lines are imaginary lines considered for the calculations and better understandings.