Question

Derive an expression for work done in sliding a body down an inclined rough plane.

Answer 1

The frictional force can be calculated by taking the product of coefficient of friction and the normal force acting over it. Find out the frictional force first. Then find the net force acting in the forward direction. And find out the work done by the body in order to move a particular displacement. These all may help you to solve this question.

Complete answer:
The body is sliding down with a force acting over it. The total force acting on the body can be shown in a diagram as,

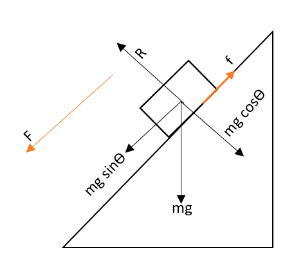
Let us assume that the frictional force acting over the body is given as $f$. This can be found by the equation,
$f=\mu N$
Here $\mu$be the coefficient of friction and $N$ be the normal force acting on the body. From the figure, we can see that this normal force is equivalent to the cosine component of the gravitational force acting. That is we can write that,
$N=mg\cos \theta$
Substituting this in the equation will give,
$f=\mu mg\cos \theta$
The resultant force in the forward direction can be written as,
$F=mg\sin \theta -\mu mg\cos \theta$
Let us assume that the distance travelled by the body down the plane is given as $S$.
Therefore the work done can be calculated as,
$W=F\cdot S$
Substituting the values in it will give the equation as,
$W=\left( mg\sin \theta -\mu mg\cos \theta \right)\cdot S$

Note:
Frictional Force is defined as the force created by two surfaces that are in contact and slide against each other. These forces are primarily affected by the nature of surface and quantity of force requiring them together. The volume of frictional force is affected by the angle and position of the object. Coefficient of friction is described as the ratio of the force needed to move the sliding surfaces over each other, and the force holding them together.