Question

Derive an expression for the velocity of the two masses ${{m}_{1}}$ and ${{m}_{2}}$ with speeds ${{u}_{1}}$ and ${{u}_{2}}$ undergoing elastic collision in one direction.

Answer 1

You could firstly recall the conservation of momentum and kinetic energy for the given case of elastic collision. Then by necessary rearrangements, you may find that the relative velocity of approach is equal to relative velocity of separation. Then by substituting accordingly in momentum conservation expression you will get the required answer.

Complete Step by step solution:
In the question, we are asked to find the expression for the velocity of two masses moving with different velocities after undergoing one dimensional elastic collision.
Let us consider two bodies with masses ${{m}_{1}}$​ and ${{m}_{2}}$​ moving with velocities ${{u}_{1}}$ and ${{u}_{2}}$ in one dimension.
These masses are undergoing collision and their velocities after collision become ${{v}_{1}}$ and ${{v}_{2}}$.

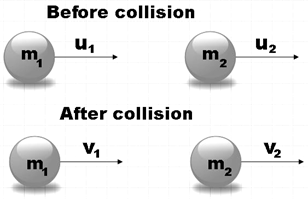
Momentum of the masses before collision is given by,
For ${{m}_{1}}$, Momentum $={{m}_{1}}{{u}_{1}}$
For ${{m}_{2}}$, Momentum $={{m}_{2}}{{u}_{2}}$ ​
So, the total momentum of the system before collision will be,
${{P}_{1}}={{m}_{1}}{{u}_{1}}+{{m}_{2}}{{u}_{2}}$

Kinetic energy of the masses before collision will be,
For ${{m}_{1}}$,
$K.E=\dfrac{1}{2}{{m}_{1}}{{u}_{1}}^{2}$
For ${{m}_{2}}$,
$K.E=\dfrac{1}{2}{{m}_{2}}{{u}_{2}}^{2}$
So, the total kinetic energy before collision could be given by,
$K.{{E}_{1}}=\dfrac{1}{2}{{m}_{1}}{{u}_{1}}^{2}+\dfrac{1}{2}{{m}_{2}}{{u}_{2}}^{2}$

Momentum of the masses after collision is given by,
For ${{m}_{1}}$, Momentum $={{m}_{1}}{{v}_{1}}$
For ${{m}_{2}}$, Momentum $={{m}_{2}}{{v}_{2}}$ ​
So, the total momentum of the system after collision will be,
${{P}_{2}}={{m}_{1}}{{v}_{1}}+{{m}_{2}}{{v}_{2}}$

Kinetic energy of the masses after collision will be,
For ${{m}_{1}}$,
$K.E=\dfrac{1}{2}{{m}_{1}}{{v}_{1}}^{2}$
For ${{m}_{2}}$,
$K.E=\dfrac{1}{2}{{m}_{2}}{{v}_{2}}^{2}$
So, the total kinetic energy before collision could be given by,
$K.{{E}_{2}}=\dfrac{1}{2}{{m}_{1}}{{v}_{1}}^{2}+\dfrac{1}{2}{{m}_{2}}{{v}_{2}}^{2}$

Now, we could use the law of conservation of momentum to get,
${{m}_{1}}{{u}_{1}}+{{m}_{2}}{{u}_{2}}={{m}_{1}}{{v}_{1}}+{{m}_{2}}{{v}_{2}}$
$\Rightarrow {{m}_{1}}\left( {{u}_{1}}-{{v}_{1}} \right)={{m}_{2}}\left( {{v}_{2}}-{{u}_{2}} \right)$ …………………………………. (1)

Then we could apply the law of conservation of kinetic energy to get,

$\dfrac{1}{2}{{m}_{1}}{{u}_{1}}^{2}+\dfrac{1}{2}{{m}_{2}}{{u}_{2}}^{2}=\dfrac{1}{2}{{m}_{1}}{{v}_{1}}^{2}+\dfrac{1}{2}{{m}_{2}}{{v}_{2}}^{2}$

$\Rightarrow {{m}_{1}}\left( {{u}_{1}}^{2}-{{v}_{1}}^{2} \right)={{m}_{2}}\left( {{v}_{2}}^{2}-{{u}_{2}}^{2} \right)$……………………………………. (2)

Diving equation (2) by equation (1), we get,
$\dfrac{{{m}_{1}}\left( {{u}_{1}}^{2}-{{v}_{1}}^{2} \right)}{{{m}_{1}}\left( {{u}_{1}}-{{v}_{1}} \right)}=\dfrac{{{m}_{2}}\left( {{v}_{2}}^{2}-{{u}_{2}}^{2} \right)}{{{m}_{2}}\left( {{v}_{2}}-{{u}_{2}} \right)}$
$\Rightarrow {{u}_{1}}+{{v}_{1}}={{v}_{2}}+{{u}_{2}}$
$\therefore {{u}_{1}}-{{u}_{2}}={{v}_{2}}-{{v}_{1}}$ ………………………………………………………………. (A)
$\Rightarrow {{v}_{2}}={{u}_{1}}-{{u}_{2}}+{{v}_{1}}$ …………………………………………….. (3)
$\Rightarrow {{v}_{1}}={{v}_{2}}-{{u}_{1}}+{{u}_{2}}$ …………………………………………….. (4)

Substituting (3) in (1), we get,

${{m}_{1}}\left( {{u}_{1}}-{{v}_{1}} \right)={{m}_{2}}\left( \left( {{u}_{1}}-{{u}_{2}}+{{v}_{1}} \right)-{{u}_{2}} \right)$
$\Rightarrow {{m}_{1}}{{u}_{1}}-{{m}_{1}}{{v}_{1}}={{m}_{2}}{{u}_{1}}-2{{m}_{2}}{{u}_{2}}+{{m}_{2}}{{v}_{1}}$
$\therefore {{v}_{1}}=\dfrac{{{m}_{1}}-{{m}_{2}}}{{{m}_{1}}+{{m}_{2}}}{{u}_{1}}+\dfrac{2{{m}_{2}}}{{{m}_{1}}+{{m}_{2}}}{{u}_{2}}$
Similarly, substituting (4) in (1), we get,
${{m}_{1}}\left( {{u}_{1}}-\left( {{v}_{2}}-{{u}_{1}}+{{u}_{2}} \right) \right)={{m}_{2}}\left( {{v}_{2}}-{{u}_{2}} \right)$
$\Rightarrow {{m}_{1}}{{u}_{1}}-{{m}_{1}}{{v}_{2}}-{{m}_{1}}{{u}_{1}}+{{m}_{1}}{{u}_{2}}={{m}_{2}}{{v}_{2}}-{{m}_{2}}{{u}_{2}}$
$\therefore {{v}_{2}}=\dfrac{2{{m}_{1}}}{{{m}_{1}}+{{m}_{2}}}{{u}_{1}}+\dfrac{{{m}_{2}}-{{m}_{1}}}{{{m}_{1}}+{{m}_{2}}}{{u}_{2}}$

Therefore, we found the velocities of the masses ${{m}_{1}}$ and ${{m}_{2}}$ after collision respectively as:

**${{v}_{1}}=\dfrac{{{m}_{1}}-{{m}_{2}}}{{{m}_{1}}+{{m}_{2}}}{{u}_{1}}+\dfrac{2{{m}_{2}}}{{{m}_{1}}+{{m}_{2}}}{{u}_{2}}$
${{v}_{2}}=\dfrac{2{{m}_{1}}}{{{m}_{1}}+{{m}_{2}}}{{u}_{1}}+\dfrac{{{m}_{2}}-{{m}_{1}}}{{{m}_{1}}+{{m}_{2}}}{{u}_{2}}$ **

Note:
It is quite obvious that you may find this derivation cumbersome. So, we could actually remember certain points and thus shorten this derivation. You could keep in mind that relative velocity of approach is always equal to relative velocity of separation for an elastic collision, that is, the expression (A) in the solution. Now, you could do substitution accordingly in conservation of momentum and thus get the required relation.