Question

Derive an expression for the time period of oscillation of a simple pendulum.

Answer 1

A simple pendulum is a system in which a mass (a bob) connected to one end of an inextensible string hanging vertically and is connected to a fixed support.
If we apply an angular displacement from the mean position, the bob will complete a left swing and a right swing and come back to its mean position again. The time taken by the pendulum for this complete cycle is known as its time period of oscillation.

Complete step by step solution:
Let us first know about a simple pendulum. It is basically a system in which a mass (a bob) is connected to one end of an inextensible string hanging vertically and is connected to a fixed support.
If we apply an angular displacement from the mean position, the bob will complete a left swing and a right swing and come back to its mean position again. The time taken by the pendulum for this complete cycle is known as its time period of oscillation.
Let a bob of mass $m$ is suspended from the end of a light inextensible string whose upper end is connected to a fixed rigid support. Now, the bob is displaced from its mean position.
Now, Using the equation of motion,
$T' - mg\cos \theta = m{v^2}l$ where $T'$ is the tension in the string, $\theta$ is the angle made by the length from vertical at any moment and $v$ is its velocity at that moment.

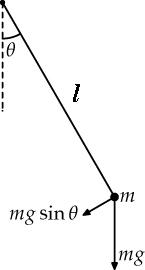
Now, the torque will tend to bring the mass to its equilibrium position,
$\tau = mgl \times \sin \theta = mg\sin \theta \times l$
As we know torque, $\tau = I\alpha$ where $I$ is the moment of inertia of the bob and $\alpha$ is its angular acceleration
So, $mg\sin \theta \times l = I \times \alpha$
For small angles of oscillations, $\sin \theta \approx \theta$
So, $I\alpha = - mgl\theta$ (Here –ve sign denotes that the torque is against the motion o bob)
As we know that the moment of inertia of the bob in this case $I = m{l^2}$
Therefore, $\alpha = - \dfrac{g}{l}\theta$
Also, $\alpha = - \omega _0^2\theta$ where ${\omega _0}$ is the angular velocity of the bob
So the equation becomes,
$- \omega _0^2\theta = - \dfrac{g}{l}\theta$
On simplifying we have
${\omega _0} = \sqrt {\dfrac{g}{l}}$
As we know time period is given by $\dfrac{{2\pi }}{{{\omega _0}}}$

So, Time period of simple pendulum $T = 2\pi \sqrt {\dfrac{l}{g}}$.

Note: There are some assumptions in the derivation of time period of a simple pendulum
1. Gravity remains constant for the system
2. There is negligible air resistance on the system
3. The length of the pendulum does not bend or compress and has negligible mass
4. The pendulum swings in a perfect plane