Question

Derive an expression for the intensity of the electric field produced by an electric dipole at a point on its axial line.

Answer 1

We will use Coulomb’s law equation to derive an expression for the intensity of the electric field. The electric fields will be calculated at a point with different distances. the expression will be the difference of these electric fields being calculated.

Formula used:
$E=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{q}{{{r}^{2}}}$

Complete step-by-step answer:
A line passing through the pair of equal and opposite charges of a dipole is called the axial line.
Consider a diagram representing the axial line of a dipole.

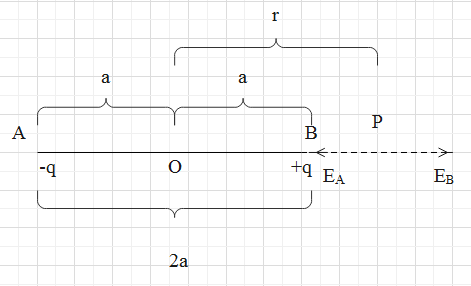
Let the charges of a dipole be represented by $-q$and $+q$. Let the distance between the charges be $2a$. Let ‘P’ be a point on the axis line at which the electric field to be determined.
Consider the figure while going through the following steps.
The electric field at a point P with the distance BP is expressed as follows.
Along the line BP due to the charge$+q$.

& {{E}_{B}}=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{q}{{{(BP)}^{2}}} \\\ & \Rightarrow {{E}_{B}}=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{q}{{{(r-a)}^{2}}} \\\ \end{aligned}$$ The electric field at a point P with the distance PA is expressed as follows. Along the line PA due to the charge $$-q$$. $$\begin{aligned} & {{E}_{A}}=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{q}{{{(AP)}^{2}}} \\\ & \Rightarrow {{E}_{A}}=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{q}{{{(r+a)}^{2}}} \\\ \end{aligned}$$ The net field at the point P is calculated as the difference between the electric fields at the distances BP and PA. Thus, the net electric field at point P is, $${{E}_{P}}={{E}_{B}}-{{E}_{A}}$$ Substitute the expressions of the electric fields at the distances BP and PA in the above equation. $${{E}_{P}}=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{q}{{{(r-a)}^{2}}}-\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{q}{{{(r+a)}^{2}}}$$ Take the common terms aside and solve further. $${{E}_{P}}=\dfrac{q}{4\pi {{\varepsilon }_{0}}}\left( \dfrac{1}{{{(r-a)}^{2}}}-\dfrac{1}{{{(r+a)}^{2}}} \right)$$ Continue the further calculation. $$\begin{aligned} & {{E}_{P}}=\dfrac{q}{4\pi {{\varepsilon }_{0}}}\left( \dfrac{4ar}{{{({{r}^{2}}-{{a}^{2}})}^{2}}} \right) \\\ & \Rightarrow {{E}_{P}}=\dfrac{2qa}{4\pi {{\varepsilon }_{0}}}\left( \dfrac{2a}{{{({{r}^{2}}-{{a}^{2}})}^{2}}} \right) \\\ \end{aligned}$$ From the diagram it’s clear that, $$2aq=p$$and the constant value $${}^{1}/{}_{4\pi {{\varepsilon }_{0}}}$$can be expressed using a variable ‘k’. So, we have the expression for the electric field at point P along the line BP as follows. $${{E}_{P}}=\dfrac{2kpr}{{{({{r}^{2}}-{{a}^{2}})}^{2}}}$$ Consider a special case, for which the condition is, $$2a << r$$, the expression for the electric field can be derived as, $${{E}_{P}}=\dfrac{2kp}{{{r}^{3}}}$$ Therefore, the expression for the intensity of the electric field produced by an electric dipole at a point on its axial line is $${{E}_{P}}=\dfrac{2kp}{{{r}^{3}}}$$. **Note:** The formula used to derive the expression is Coulomb’s law for a point charge. This is because we will be solving the electric field at a point, but considering two different distances. If the electric field is given to be within the distance between the charges of a dipole, then, the final expression should be used as discussed above.