Question

Derive an expression for the force per unit length between two straight parallel conductors carrying current. Hence define ampere.

Answer 1

Placed two long thin straight conductors parallel to each in vacuum carrying current.

Complete step by step solution:

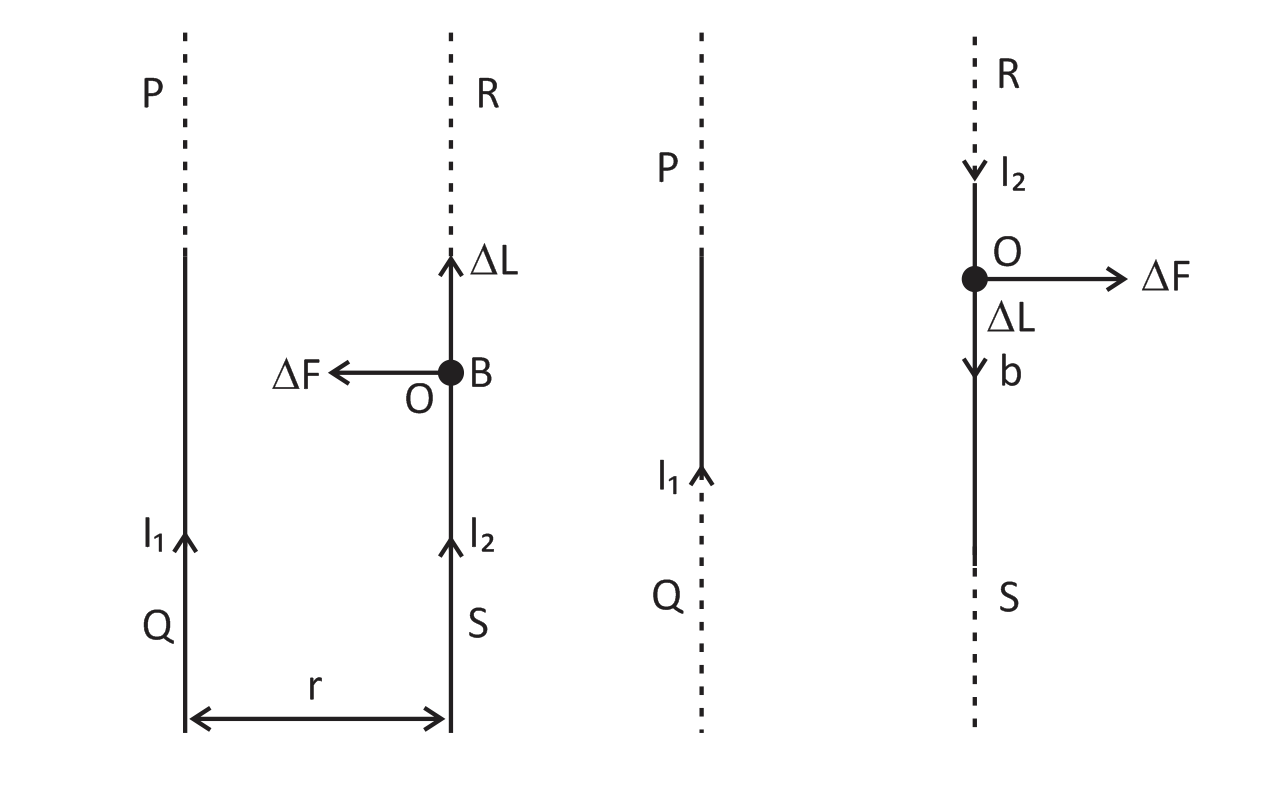
Force per unit length between two long straight parallel conductors. Suppose two thin straight conductors (or wires) PQ and RS are placed parallel to each other in vacuum (or air) carrying current ${I_1}\;and\;{I_2}$ respectively. It has been observed experimentally that when the currents in the wire in the same direction, they experience an attractive force and when they carry current in opposite directions, they experience a repulsive force. Let the conductors PQ and RS carry currents ${I_1}\;and\;{I_2}$ in the same direction and placed at separation r.
${B_1} = \dfrac{{{\mu _0}{I_1}}}{{2\pi r}}$
$\Delta F = {B_1}{I_1}\;\Delta L\;\sin \;90^\circ$
${B_1} = \dfrac{{{\mu _0}{I_1}}}{{2\pi r}}{I_2}\;\Delta L$
$F = \dfrac{{{\mu _0}{I_1}{I_2}}}{{2\pi r}}\sum {\Delta L} = \dfrac{{{\mu _0}{I_1}{I_2}}}{{2\pi r}}L$
$\dfrac{F}{L} = \dfrac{{{\mu _0}{I_1}{I_2}}}{{2\pi r}}N/m$

Consider a current-element ‘ab’ of length $\Delta L$ of wire RS. The magnetic field produced by current carrying conductor PQ at the location of other wire RS.

According to Maxwell’s right hand rule or right hand Palm rule no. 1, the direction of B1 will be perpendicular to the plane of paper and directed downward. Due to this magnetic field, each element of another wire experiences a force. The direction of the current element is perpendicular to the magnetic field; therefore the magnetic force on element AB of length $\Delta L$.

Definition of ampere: Fundamental unit of current ampere has been defined assuming the force between the two current carrying wires as standard. The force between two parallel current carrying conductor of separation r is
$\dfrac{F}{L} = \dfrac{{{\mu _0}{I_1}{I_2}}}{{2\pi R}}N/m$
$F = \dfrac{{{\mu _0}}}{{2\pi }} = 2 \times {10^{ - 7}}N/m$

Thus 1 ampere is the current which when flowing in each of parallel conductors placed at separation 1 m in vacuum exert a force of $2 \times {10^{ - 7}}$ on 1m length of either wire.

Note: The ratio F/I is the force per unit length between two parallel current ${I_1}\;and\;\;{I_2}$ separated by a distance r. The force is attractive if the currents are in the same direction and repulsive, if they are in opposite directions.