Question

Derive an expression for the electric potential at a point along the axial line of an electric dipole. At a point charge, the values of the electric field and potential are $25N/C$and $10J/C$. Then calculate:
A. the magnitude of the charge
B. distance of the charge from the point of observation

Answer 1

We know that the electric potential due to a charge, is defined as the amount of energy needed to move a unit positive charge to infinity. Also the potential at any point is the vector sum of potentials at that point. Also, potential is proportional to the charge and inversely proportional to the square of the distance between the point and the charge.

Formula used:
$x=\dfrac{V_{X}}{E_{X}}$ and $V=\dfrac{Kq}{r}$

Complete step by step answer:
Consider an electric dipole $AB$ of length $a$ and let $X$ be a point on the axial line such that it is at a distance $x$ from the centre of the dipole $AB$.

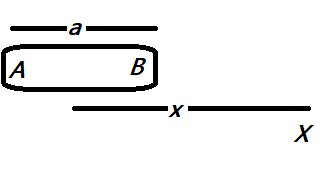
Then the electric potential at the point $X$ is given as,$V_{X}=V_{+q}+V_{-q}$
Or, $V_{X}=K\left[\dfrac{q}{x-a}+\dfrac{-q}{x+a}\right]=\dfrac{K(2qa)}{x^{2}-a^{2}}=\dfrac{KP}{x^{2}-a^{2}}$, where $P$ is the dipole moment of the electric dipole $AB$of length $a$ and $K$ is the coulombs constant which is equal to $9\times 10^{9}Nm^{2}/C$

Given that , the electric potential $V_{X}=10J/C$ and the electric field $E_{X}= 25N/C$
Then we know that, $E=\dfrac{V}{r}$ where $r$ is the distance of the charge, substituting the values, we get, $x=\dfrac{V_{X}}{E_{X}}$

Then, we get $x=\dfrac{10}{25}=0.4m$
i.e the distance of the $X$ from the from the centre is $0.4m$
Also from the definition of electric potential, we know that , $V=\dfrac{Kq}{r}$ , then substituting the values we get,

$q=\dfrac{V_{X}x}{K}=\dfrac{10\times 0.4}{9\times 10^{9}}=4.45 \times 10^{-10}C$
i.e. the magnitude of each charge is $4.45\times 10^{-10}C$

Hence the answers are as follows:
A. the magnitude of each charge is $4.45\times 10^{-10}C$ and
B. the distance of the $X$ from the from the centre is $0.4m$

Note:
To find the charge you can also use the $E_{X}$ as $E_{X}=\dfrac{Kq}{x^{2}}$. Also, the value of charge $q$ calculated here, is only one charge of the dipole. Note the dipole moment $P=2aq$. This is taken for simplification and easy calculations. Also, $K=\dfrac{1}{4\pi \epsilon_{0}}$.