Question

Derive an expression for the electric field intensity at a point on the equatorial line of an electric dipole of dipole moment $\vec P$ and length $2a$. What is the direction of this field?

Answer 1

A dipole consists of two equals charges separated at a distance but with opposite sign. Equatorial line is the perpendicular line drawn from the centre of the dipole. We will find electric fields due to both charges of dipole at equatorial point and will add them using vector algebra.

Formula used:
Dipole moment $\vec P = q \times 2a$, { $q$ is charge and $2a$ is half distance of dipole}
Electric field intensity $E = \dfrac{1}{{4\pi {\varepsilon _0}}} \times \dfrac{q}{{{r^2}}}$ { $q$ is charge and $r$ is distance of given point}

Complete step by step answer:
Let us first draw the diagram.

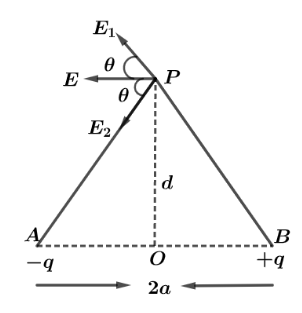
From the diagram we can see, Net electric field intensity will only have horizontal components of $E\cos \theta$. And Now,
In triangle AOP and POB,
${(AP)^2} = {(BP)^2} = ({d^2} + {a^2})$
And, $< PAO = \theta$ {by vertically opposite angle}
So, $\cos \theta = \dfrac{1}{{{{({d^2} + {a^2})}^{\dfrac{1}{2}}}}}$
Now, we will calculate electric field intensity due to both charges at point P
Electric field $E1$ at point P due to $- q$ along AP is given by,
$E_1 = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{q}{{{{(AP)}^2}}}$
$\Rightarrow E_1 = k \times \dfrac{q}{{{{({d^2} + {a^2})}^2}}}$, where { $k = \dfrac{1}{{4\pi {\varepsilon _0}}}$} $\to (i)$
Similarly, Electric field along PB is given by,
$E_2 = k \times \dfrac{q}{{{{(PB)}^2}}}$
$\Rightarrow E_2 = k \times \dfrac{q}{{{{({d^2} + {a^2})}^2}}}$ $\to (ii)$
Since, $E_1 = E_2$ say $E$
Net electric field at point P will be the sum of $E\sin \theta$ components and $E\cos \theta$components but as we see from the diagram that vertical components will be cancelled, only horizontal components will be added. Hence, net electric field intensity at point P is given by,
${E_p} = 2E\cos \theta$
$\Rightarrow {E_p} = 2 \times k \times \dfrac{q}{{{{({d^2} + {a^2})}^2}}} \times \dfrac{1}{{{{({d^2} + {a^2})}^{\dfrac{1}{2}}}}}$ {$\cos \theta = \dfrac{1}{{{{({d^2} + {l^2})}^{\dfrac{1}{2}}}}}$}
For small dipole where, $a < < < d$
Hence, electric field intensity at equatorial point is given by,
$\therefore {E_p} = - \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{\vec P}}{{{d^3}}}$.
And the direction of the electric field is always opposite to that of the electric dipole.

Note: The direction of electric dipole is always taken as from negative charge to the positive charge , here this direction became from A to B and electric field as calculated is in direction from B to A, This shows that direction of electric field at point P is in opposite direction of Dipole moment.