Question

Derive an expression for the capacitance of a parallel plate capacitor.

Answer 1

Whenever a potential difference is applied across the plates of the capacitors, the current flows in the circuit developing positive charge on one plate and negative charge on the other plate. Consider a parallel plate capacitor with two parallel plates possessing charges $+ Q$ and $- Q$ on them. As the charges are induced due to the potential difference, they will be a function of voltage. The charge on a plate is given as $Q = CV$. Now, find the potential difference between the plates using the electric field as it will be by $V = \int {{\mathbf{E}}.{\mathbf{dr}}}$, from this, you can find the charge induced on the plate.

Complete step by step answer:
Let the area of the plates be $A$ and the separation between them be $d$. The charges $+ Q$ and $- Q$ will appear on the faces. The magnitude of the charge density $\sigma$ will be given by $\sigma = \dfrac{Q}{A}$ for each plate.

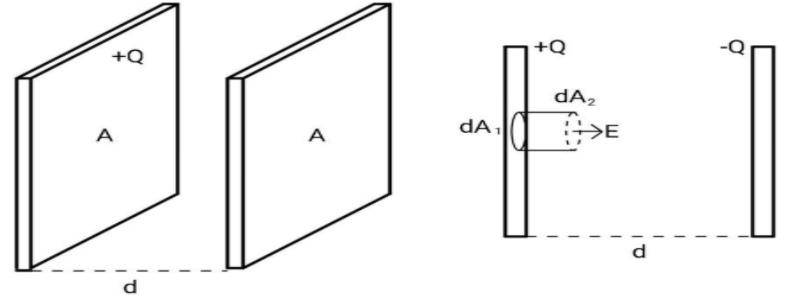
The cylindrical surface is the gaussian surface which will be used to find the electric field. As the electric field inside a conductor is zero, the flux through $d{A_1}$ will be zero. The electric field near the surface of a plane is perpendicular to the surface. Hence, the flux through the curved surface will also be zero.
Now, the electric field through $d{A_2}$ will be given by Gauss's Law.
$\oint {{{\mathbf{E}}_{\mathbf{1}}}.{\mathbf{d}}{{\mathbf{A}}_{\mathbf{1}}}} + \oint {{{\mathbf{E}}_{\mathbf{2}}}.{\mathbf{d}}{{\mathbf{A}}_{\mathbf{2}}}} + \oint {{{\mathbf{E}}_{\mathbf{3}}}.{\mathbf{d}}{{\mathbf{A}}_{\mathbf{3}}}} = \dfrac{Q}{{{\varepsilon _0}}}$
${{\mathbf{E}}_{\mathbf{1}}} = 0$ and ${{\mathbf{E}}_{\mathbf{3}}} = 0$
$\Rightarrow \oint {{{\mathbf{E}}_{\mathbf{2}}}.{\mathbf{d}}{{\mathbf{A}}_{\mathbf{2}}}} = \dfrac{Q}{{{\varepsilon _0}}}$
Here, the angle between the field and the area vector will be zero as both will be perpendicular to the plate.
And, also the electric field is constant.
${E_2}dA = \dfrac{{dq}}{{{\varepsilon _0}}} \\\ \because dq = \sigma dA \\\ \Rightarrow {E_2}dA = \dfrac{{\sigma dA}}{{{\varepsilon _0}}} \\\ \Rightarrow {E_2} = \dfrac{\sigma }{{{\varepsilon _0}}} \\\ \Rightarrow {E_2} = \dfrac{Q}{{{\varepsilon _0}A}} \\\$
Therefore, the electric field is given by${E_2} = \dfrac{Q}{{{\varepsilon _0}A}}$.

Now, the potential difference will be $V = \int {{\mathbf{E}}.{\mathbf{dr}}}$.
$\Rightarrow V = \int {Edr} \\\ \Rightarrow V = \int {\dfrac{Q}{{{\varepsilon _0}A}}} dr \\\ \Rightarrow V = \dfrac{Q}{{{\varepsilon _0}A}}\int {dr} \\\ \Rightarrow V = \dfrac{{Qd}}{{{\varepsilon _0}A}} \\\$
Comparing from the equation $Q = CV$
The capacitance will be given by
$C = \dfrac{Q}{V} \\\ C = \dfrac{Q}{{\dfrac{{Qd}}{{{\varepsilon _0}A}}}} \\\ \Rightarrow C = \dfrac{{{\varepsilon _0}A}}{d} \\\$
Hence, the capacitance of a parallel plate capacitor is given by $C = \dfrac{{{\varepsilon _0}A}}{d}$.

Note:
The electric field near a small surface is always perpendicular, there will not be any horizontal component of the electric field. The above method of finding capacitance is always applicable. For example, consider a cylinder with internal radius ${r_1}$ and external radius ${r_2}$. You imagine a cylindrical gaussian surface and find the electric field as a function of the radial distance from the axis and also consisting of the total charge $Q$. Then you find the potential difference between the outer and the inner surface, and then from the formula, you simply find the capacitance. Keep in mind that this method is not always easy.