Question

Derive an expression for mechanical force per unit area of surface charge density.

Answer 1

The quantity of charge contained per unit area is called surface charge density. All charged conductors will experience some mechanical force. Elements having a surface charge density will always experience a mechanical force outwards. Here we have to derive an expression for the mechanical force.

Complete step by step answer:
Small elements of the conductor will experience a mechanical force normally outwards. Let us consider the small element $dS$ as shown below,

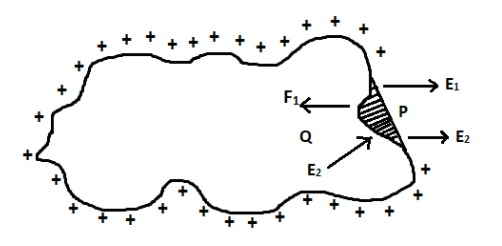
Let $\sigma$ be the surface charge density of the conductor. Then the charge carried by the small element $dS$ be $dq$.
Then we can write,
$dq = \sigma dS$ -------$(1)$
Let us consider a point $P$ outside the small element as shown in the figure.
At this point $P$, the electrical intensity can be written as,
$E = \dfrac{\sigma }{{{\varepsilon _0}k}}$ -------$(2)$
where ${\varepsilon _0}$ stands for the permittivity of free space and $k$ stands for the dielectric constant.

The electrical intensity is directed normally outwards.
The electrical intensity $E$ can be resolved into two components, ${E_1}$ and ${E_2}$.
$\overrightarrow {{E_1}}$ is the component of electrical intensity due to the small charge $dq$present in the element.
${\vec E_2}$ is the component due to the rest of the charges present on the surface.
Hence the total electrical intensity at the point $P$ can be written as,
$E = {E_1} + {E_2}$
Substituting this value in equation $(2)$
${E_1} + {E_2} = \dfrac{\sigma }{{{\varepsilon _0}k}}$ --------$(3)$

Let us now consider the point $Q$. At this point, the components of electrical intensity are in opposite direction. Inside the charged conductor the total charge is zero.
i.e.
${E_1} - {E_2} = 0$
$\therefore {E_1} = {E_2}$
Substituting ${E_1} = {E_2}$ in equation $(3)$
We get
${E_2} + {E_2} = \dfrac{\sigma }{{{\varepsilon _0}k}}$
This can be written as,
$2{E_2} = \dfrac{\sigma }{{{\varepsilon _0}k}}$
From this, we can write ${E_2}$ as,
${E_2} = \dfrac{\sigma }{{2{\varepsilon _0}k}}$
We know that the electrical intensity due to the rest of the charges in the conductor is ${E_2}$. The element $dS$ of the conductor will experience a repulsive force due to this component.

The repulsive force experienced by the rest of the conductor due to the charge $dq$ in the small element $dS$ is given by,
$F = {E_2}dq$
We know that ${E_2} = \dfrac{\sigma }{{2{\varepsilon _0}k}}$
and $dq = \sigma dS$
Substituting these values in the equation for force,
$F = \dfrac{\sigma }{{2{\varepsilon _0}k}}.\sigma .ds = \dfrac{{{\sigma ^2}}}{{2{\varepsilon _0}k}}dS$
From this equation, we can write
$\dfrac{F}{{dS}} = \dfrac{{{\sigma ^2}}}{{2{\varepsilon _0}k}}$
The force per unit area can be written as, $\dfrac{F}{{dS}} = f$
Thus the above equation will become,
$f = \dfrac{{{\sigma ^2}}}{{2{\varepsilon _0}k}}$
This is the mechanical force per unit area of a conductor due to a surface charge density.

Note: The S.I unit for the mechanical force per unit area is given by $N/{m^2}$. Like charges repel each other and unlike charges attract. In a charge-carrying conductor, the charges are all similar. Hence when we consider a small element the rest of the conductor will experience the mechanical force due to the repulsion of like charges.