Solveeit Logo
Login

Question

Question: Derive an expression for maximum height and range of an object in projectile motion....

Derive an expression for maximum height and range of an object in projectile motion.

Explanation

Solution

As, here in this question, we need to derive the expression for maximum height and range of an object in projectile motion, we need to have a clear concept of the parabolic motion. We need to find out the trajectory or the path followed in a projectile motion. After that we need to use the components of the velocity vector in order to derive the expression for maximum height and range of an object in projectile motion. Also, we need to use Newton's equation of motion.

Complete answer:
Step one
__
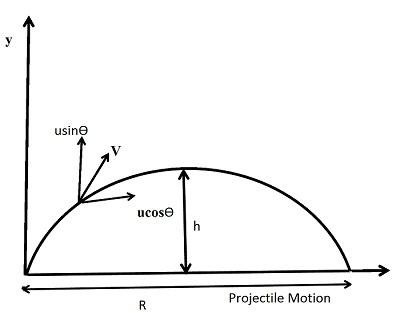
The horizontal component of velocity is given by, vx=ucos⁡θ{v_x} = u\cos \theta
The vertical component of the velocity is given by, vy=usin⁡θ{v_y} = u\sin \theta
Let us assume that the body reaches the point P(x,y), after time tt
Also, let us assume the maximum height to be H
Now, if we need to find the Horizontal distance, we can write the equation for it as,
x=ucos⁡θtx = u\cos \theta t ………(i) As, distance = speed ×\timestime
Step two
Now, for maximum height of an object for projectile motion can be found by using third equation of motion, v2−u2=2as{v^2} - {u^2} = 2as
So, putting the values in the above equation, we get,
o2−(usin⁡θ)2=2(−g)H{o^2} - {(u\sin \theta )^2} = 2( - g)H
⇒H=−u2sin⁡2θ−2g\Rightarrow H = \dfrac{{ - {u^2}{{\sin }^2}\theta }}{{ - 2g}}
∴H=u2sin⁡2θ2g\therefore H = \dfrac{{{u^2}{{\sin }^2}\theta }}{{2g}}
Step three
Let the horizontal range be R
We know that time of flight, T=2usin⁡θgT = \dfrac{{2u\sin \theta }}{g}
Now, using equation (i) we can write,
R=ucos⁡θTR = u\cos \theta T
⇒R=ucos⁡θ×2usin⁡θg\Rightarrow R = u\cos \theta \times \dfrac{{2u\sin \theta }}{g}
∴R=u2sin⁡2θg\therefore R = \dfrac{{{u^2}\sin 2\theta }}{g}
Hence, the required value of maximum height is u2sin⁡2θ2g\dfrac{{{u^2}{{\sin }^2}\theta }}{{2g}} and the range is u2sin⁡2θg\dfrac{{{u^2}\sin 2\theta }}{g}.

Note:
We should not confuse time of maximum height with time of flight. Time of maximum height is the time when the object attains the maximum height and is given by t=usin⁡θgt = \dfrac{{u\sin \theta }}{g}. Time of flight is the total time taken by the object to cover the total horizontal distance or in other words the time till when the object is in air and is given by T=2usin⁡θgT = \dfrac{{2u\sin \theta }}{g}.