Question

Derive an expression for magnetic field strength at any point on the axis of a circular current carrying loop using Biot-Savart’s law.

Answer 1

Biot Savart’s law gives us the relationship between magnetic field, current in the element, length of the element, angle between the line joining element to the point and element and distance between point and element. Using Biot-Savart’s law, we can calculate the expression for magnetic fields for different objects.

Complete step-by-step solution:
According to the Biot Savart’s law, the magnetic field due to a current carrying element is directly proportional to the number of turns in the element, the current flowing through it and inversely proportional to the distance between the point at which the magnetic field is to be measured and the element.
$B\propto \dfrac{IdL\sin \theta }{{{r}^{2}}}$
Here,
$N$ is the number of turns
$I$ is the current in the element
$dL$ is the length of the element
$r$ is the distance between point and element
$\theta$ is the angle between element $dL$ and the line joining it to the point
On removing the sign of proportionality we get,
$B=\dfrac{{{\mu }_{0}}IdL\sin \theta }{4\pi {{r}^{2}}}$
$\dfrac{{{\mu }_{0}}}{4\pi }$ is the constant of proportionality , here ${{\mu }_{0}}$ is the permittivity of free space.

For magnetic field on the axis of a circular loop

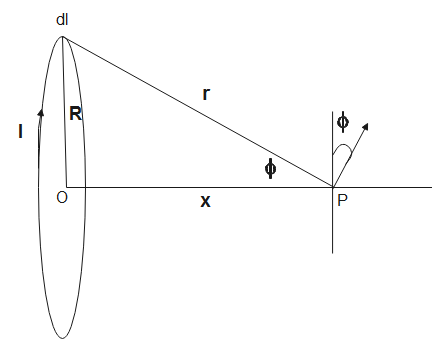
Let the magnetic field due to element $dl$ be , therefore,
$dB=\dfrac{{{\mu }_{0}}Idl\sin (\phi )}{4\pi }$

Integrating to find for the loop, we get,
$\begin{aligned} & \int\limits_{0}^{B}{dB}=\dfrac{{{\mu }_{0}}I\sin (\phi )}{4\pi {{R}^{2}}}\int\limits_{0}^{2\pi R}{dl} \\\ & \Rightarrow B=\dfrac{{{\mu }_{0}}I\sin \phi }{4\pi {{r}^{2}}}\left[ l \right]_{0}^{2\pi R} \\\ & \Rightarrow B=\dfrac{{{\mu }_{0}}I\sin \phi }{4\pi {{r}^{2}}}2\pi R \\\ & \therefore B=\dfrac{{{\mu }_{0}}I\sin \phi R}{2{{r}^{2}}} \\\ \end{aligned}$

When we substitute, $\sin \phi =\dfrac{R}{r}$ in the above equation, we get,
$\Rightarrow B=\dfrac{{{\mu }_{0}}IxR}{2{{r}^{3}}}$

From the triangle $r=\sqrt{{{x}^{2}}+{{R}^{2}}}$, we substitute $r$ to get,
$\therefore B=\dfrac{{{\mu }_{0}}I{{R}^{2}}}{2{{({{x}^{2}}+{{R}^{2}})}^{\dfrac{3}{2}}}}$

Therefore, the magnetic field on the axis of a circular loop is $\dfrac{{{\mu }_{0}}I{{R}^{2}}}{2{{({{x}^{2}}+{{R}^{2}})}^{\dfrac{3}{2}}}}$.

Note:
When the value of $x$ becomes zero, we get the expression for the magnetic field at the centre of the loop. Here, we can form a small element on the wire and integrate it for the whole loop. We calculate the direction of the magnetic field at a point on the axis using the right hand thumb rule. It states that if the thumb points in the direction of flow of current, then the fingers show the direction of the magnetic field.