Question

Derive an expression for magnetic field at a point on the axial line of a bar magnet.

Answer 1

First of all, we will draw the schematic diagram of the bar magnet and the point, with all the parameters shown. Then we will find the magnetic field for the individual poles. After that we will find the resultant magnetic field on the point, after manipulating accordingly.

Formula used:
The formula which gives the magnetic field at a certain distance is as follows:
$B = \dfrac{{{\mu _0}}}{{4\pi }} \times \dfrac{m}{{{x^2}}}$ …… (1)
Where,
$B$ indicates the magnetic field.
${\mu _0}$ indicates absolute permeability of free space.
$m$ indicates the magnetic strength of each pole.
$x$ indicates the distance of the pole from the point.

Complete step by step answer:
In the given question, we are supplied with the following data:
There is a bar magnet and there is another point on the axial line of the bar magnet. We are asked to find the expression for the magnetic field at a point on the axial line of a bar magnet.

To begin with, we will draw a diagram for the better understanding, as shown below:

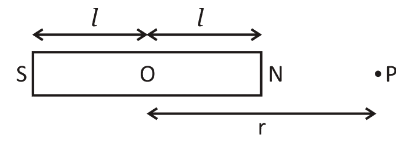
Let ${\text{NS}}$ be a $2l$ length magnetic bar magnet with each pole of magnetic strength $m$. ${\text{O}}$ is the magnet centre, and ${\text{P}}$ is a point at which the magnetic field has to be measured on the axial line at a distance $r$ from the magnet centre ${\text{O}}$.

From the diagram, the distance of the point from the north pole is $r - l$.
The magnetic field ${B_1}$ at ${\text{P}}$ due to north pole of the magnet can be written as:
${B_1} = \dfrac{{{\mu _0}}}{{4\pi }} \times \dfrac{m}{{{{\left( {r - l} \right)}^2}}}$ …… (2)
Again, the distance of the point from the south pole of the magnet is $r + l$.
The magnetic field ${B_2}$ at ${\text{P}}$ due to north pole of the magnet can be written as:
${B_2} = \dfrac{{{\mu _0}}}{{4\pi }} \times \dfrac{m}{{{{\left( {r + l} \right)}^2}}}$ …… (3)

Now, we can find the resultant magnetic field at the point ${\text{P}}$. It can be clearly seen that ${B_1} > {B_2}$. So, we can write:
B = {B_1} - {B_2} \\\ \Rightarrow B = \dfrac{{{\mu _0}}}{{4\pi }} \times \dfrac{m}{{{{\left( {r - l} \right)}^2}}} - \dfrac{{{\mu _0}}}{{4\pi }} \times \dfrac{m}{{{{\left( {r + l} \right)}^2}}} \\\ \Rightarrow B = \dfrac{{{\mu _0}}}{{4\pi }} \times \left[ {\dfrac{m}{{{{\left( {r - l} \right)}^2}}} - \dfrac{m}{{{{\left( {r + l} \right)}^2}}}} \right] \\\ \Rightarrow B = \dfrac{{{\mu _0}}}{{4\pi }} \times \left[ {\dfrac{{\left( {2rl + 2rl} \right) \times m}}{{{{\left( {{r^2} - {l^2}} \right)}^2}}}} \right] \\\ \Rightarrow B = \dfrac{{{\mu _0}}}{{4\pi }} \times \left[ {\dfrac{{4rlm}}{{{{\left( {{r^2} - {l^2}} \right)}^2}}}} \right] \\\ \Rightarrow B = \dfrac{{{\mu _0}}}{{4\pi }} \times \left[ {\dfrac{{\left( {2l} \right)m \times 2r}}{{{{\left( {{r^2} - {l^2}} \right)}^2}}}} \right] \\\
Again, we know, magnetic moment is given by:
$M = m \times 2l$

Now, we can modify the expression for the magnetic field as:
$\therefore B = \dfrac{{{\mu _0}}}{{4\pi }} \times \left[ {\dfrac{{2Mr}}{{{{\left( {{r^2} - {l^2}} \right)}^2}}}} \right]$

Hence, the above expression is for the magnetic field at a point on the axial line of a bar magnet.

Note: While solving this problem, it should be remembered that at an axial point, the magnetic field has the same direction as that of the magnetic dipole moment vector due to a bar magnet. Since, the north pole is nearer to the point, so its magnetic field at that point is higher than the south pole.