Question

Derive an expression for electric potential at a point due to an electric dipole. Discuss its special cases.

Answer 1

An electric dipole is a set of charges that have an equal magnitude but opposite polarity or sign. The two charges are separated by a certain distance between them.

Formula used: In this solution, we will use the following formula:
Electric potential due to a charge $V = \dfrac{{kQ}}{r}$ where $Q$ is the charge and $r$ is the distance of the point from the charge.

Complete step by step answer
Let us start the solution by drawing a schematic diagram of a dipole and the point P where we want to find the electric potential.

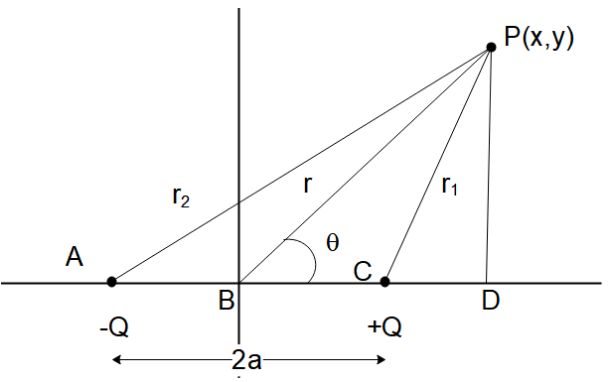
The potential at point P due to charge $+ Q$ will be: ${V_1} = \dfrac{{KQ}}{{{r_1}}}$
The potential at point P due to charge $- Q$ will be: ${V_2} = - \dfrac{{KQ}}{{{r_2}}}$
Since the potentials are scalar, they add up at point P and the net potential will be
$\Rightarrow V = {V_1} + {V_2}$
$\Rightarrow V = \dfrac{{KQ}}{{{r_1}}} - \dfrac{{KQ}}{{{r_2}}}$
Which can also be written as,
$\Rightarrow V = KQ\left( {\dfrac{1}{{{r_1}}} - \dfrac{1}{{{r_2}}}} \right)$
But we want to find the potential in terms of known quantities. In this case, the known quantities are the distance of the point from the centre of the dipole and the angle the line joining the centre of the dipole, and the point form with the axis of the dipole i.e. $r$ and $\theta$ which are shown in the image.
So, in the triangle PCD, since it is a right-angled triangle, we can write
$\Rightarrow {r_1}^2 = {(x - a)^2} + {y^2}$
And similarly, for triangle PAD,
$\Rightarrow {r_2}^2 = {(x + a)^2} + {y^2}$
Opening the brackets for both these terms, we get
$\Rightarrow {r_1}^2 = {x^2} - 2ax + {a^2} + {y^2}$ and
$\Rightarrow {r_2}^2 = {x^2} + 2ax + {a^2} + {y^2}$
Since we know that $\cos \theta = x/r$
$\Rightarrow x = r\cos \theta$, and ${x^2} + {y^2} = {r^2}$ we can simplify ${r_1}$ and ${r_2}$ as:
$\Rightarrow {r_1}^2 = {r^2} - 2ar\cos \theta + {a^2}$ and
$\Rightarrow {r_2}^2 = {r^2} + 2ar\cos \theta + {a^2}$
Since we are finding the potential at a point which is far from the dipole so that $r > > > a$, we can simplify further as
$\Rightarrow {r_1}^2 = {r^2} - 2ar\cos \theta$
$\Rightarrow {r_2}^2 = {r^2} + 2ar\cos \theta$
Taking out ${r^2}$ common in both terms, we get
$\Rightarrow {r_1}^2 = {r^2}\left( {1 - \dfrac{{2a\cos \theta }}{r}} \right)$
$\Rightarrow {r_2}^2 = {r^2}\left( {1 + \dfrac{{2a\cos \theta }}{r}} \right)$
Since we want to actually find out ${r_1}$ and ${r_2}$, we can take the square root on both sides as:
$\Rightarrow {r_1} = r{\left( {1 - \dfrac{{2a\cos \theta }}{r}} \right)^{1/2}}$
$\Rightarrow {r_2} = {r^2}{\left( {1 + \dfrac{{2a\cos \theta }}{r}} \right)^{1/2}}$
Since $a/r < < 1$, we can use a binomial expansion approximation ${(1 + x)^n} = 1 + nx$
So,
$\Rightarrow {r_1} = r - a\cos \theta$ and
$\Rightarrow {r_2} = r + a\cos \theta$
Now we can calculate the net potential substituting ${r_1}$ and ${r_2}$ in equation (1) as:
$\Rightarrow V = KQ\left( {\dfrac{1}{{r - a\cos \theta }} - \dfrac{1}{{r + a\cos \theta }}} \right)$
Simplifying this term, we get
$\Rightarrow V = KQ\left( {\dfrac{{2a\cos \theta }}{{{r^2} - {a^2}{{\cos }^2}\theta }}} \right)$
We can write the dipole moment $p = 2aQ$ so
$\Rightarrow V = \left( {\dfrac{{Kp\cos \theta }}{{{r^2} - {a^2}{{\cos }^2}\theta }}} \right)$
The special cases are:
1.) When the point is on the axis of the dipole i.e. $\theta = 0$ i.e. $\cos \theta = 1$
$\Rightarrow V = \left( {\dfrac{{Kp}}{{{r^2} - {a^2}}}} \right)$
2.) When the point is perpendicular to the axis of the dipole $\theta = 90^\circ$ i.e. $\cos \theta = 0$
$\Rightarrow V = 0$.

Note
There are a lot of trigonometric identities and approximations that we use in this solution which can be effectively done after deriving this expression multiple times. Molecules in nature are often treated as dipoles to find the electric fields and electric potentials at any point so it is helpful to know the electric potentials of dipoles.