Question

Derive an expression for bandwidth of interference fringes in Young’s double slit experiment?

Answer 1

First of all, we will find the path difference, then we find the conditions for constructive and destructive interferences. We will find the bandwidth by calculating the difference between the two consecutive fringes.

Complete step by step answer:
We are asked to derive the expression for bandwidth of interference fringes in Young’s double experiment:
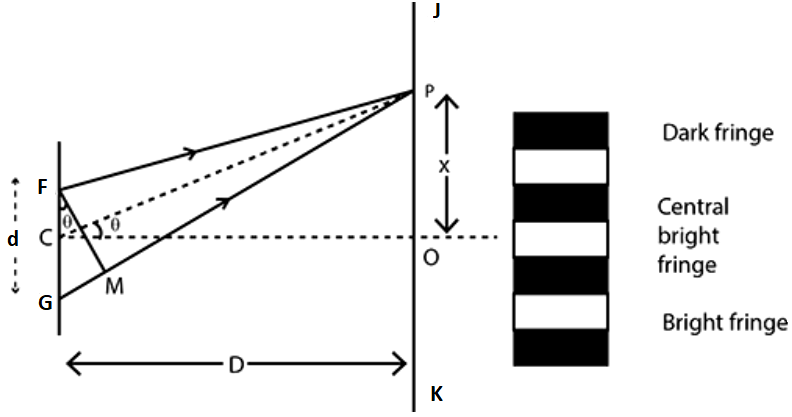
For this, let us assume the distance between two coherent sources ${\text{F}}$ and ${\text{G}}$
be d. The wavelength of the light is $\lambda$. Screen ${\text{JK}}$ is placed parallel to ${\text{FG}}$ which is at a distance of ${\text{D}}$ from the coherent sources ${\text{F}}$
and ${\text{G}}$. ${\text{C}}$ is taken as the midpoint of ${\text{FG}}$.
Point ${\text{O}}$ is a taken on the screen equidistant from ${\text{F}}$ and ${\text{G}}$. ${\text{P}}$ is a point which is at a distance of $x$ from ${\text{O}}$, as illustrated in figure below The waves coming from ${\text{F}}$ and ${\text{G}}$ meet at ${\text{P}}$.

For the interference bandwidth:
Draw ${\text{FM}}$ upon ${\text{GP}}$ such that both are perpendicular to each other.

The path difference is given by:
${\text{S}} = {\text{GP}} - {\text{FP}}$

Since, we know,
${\text{FP}} = {\text{MP}}$

$$\therefore \delta = {\text{GP}} - {\text{FP}} \\\ = {\text{GP}} - {\text{MP}} \\\ = {\text{GM}} \\\$$

In the $\Delta {\text{FGM}}$ :

$$\sin \theta = \dfrac{{{\text{GM}}}} {d} \\\ {\text{GM}} = d\sin \theta \\\$$

In case the angle is very small, then we can write:
$\sin \theta = \theta$

So, the path difference can be now written as:
$\delta = \theta d$

Again, in the triangle ${\text{COP}}$, we have:

$$\tan \theta = \dfrac{{{\text{OP}}}} {{{\text{CP}}}} \\\ \tan \theta = \dfrac{{xd}} {{\text{D}}} \\\$$

The condition for constructive interference, with path difference $n\lambda$.
Where, $n$ indicates the order of the bright fringes.
We can write:

$$\mu \dfrac{{xd}} {{\text{D}}} = \lambda \\\ x = \dfrac{{\text{D}}} {d}\lambda \\\$$

The above equation gives us the distance between the ${n^{th}}$ bright fringe and the point ${\text{O}}$.

The condition for dark fringes, with path difference $\left( {2n - 1} \right)\dfrac{\lambda }{2}$.
Where, $n$ indicates the order of the dark fringes.
So, we can write:
$x = \dfrac{{\text{D}}}{d}\left( {2n - 1} \right)\dfrac{\lambda }{2}$

The above equation gives the distance between the ${n^{th}}$ bright fringe and the point ${\text{O}}$.

We know, the bandwidth $\left( \beta \right)$ is defined as the distance between two consecutive dark or bright bands. The consecutive bright fringes with the orders ${\left( {n + 1} \right)^{th}}$ and ${n^{th}}$ is the bandwidth.
So, we can write:
$\beta = \dfrac{{\text{D}}} {d}\left( {n + 1} \right)\lambda - \dfrac{{\text{D}}} {d}n\lambda \\\ \implies \beta = \dfrac{{\text{D}}} {d}\lambda n + \dfrac{{\text{D}}} {d}\lambda - \dfrac{{\text{D}}} {d}\lambda n \\\ \therefore \beta = \dfrac{{\text{D}}} {d}\lambda \\\$

Hence, the bandwidth is given by $\dfrac{{\text{D}}}{d}\lambda$.

Note:
To solve this problem to derive the expression of bandwidth, you should have firm knowledge of interferences of light waves. It is important to find the path difference to proceed further in the solution. While calculating the bandwidth, always remember that it is the distance between the consecutive bright fringes or dark fringes.