Question

Derive an expression for an equivalent focal length of two thin lenses kept in contact.

Answer 1

Focal length is the distance over which the parallel rays either converge or diverge. For convex lenses, the focal length is positive and for concave length it is negative. Focal length varies with sign depending on the nature of the lens and the mirror.

Complete solution:

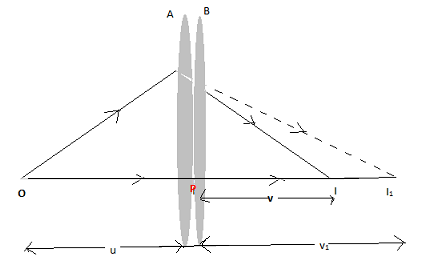
Let us consider two lenses A and B of focal length $f_1$ and $f_2$ which are placed in contact with each other. The object is placed at a point O beyond the focus of the first lens A. $I_1$ is the image produced by the first lens which is real. Since it is a real image, it serves as a virtual object for the second lens B producing the final image at $I$. The direction of the rays emerging from the first lens gets changed according to the angle at which strikes the second lens. We assume that the optical centers of the lenses are coincident as the lenses are very thin. Let this central point be represented by P.
Therefore, For the image formed by lens A, we get
\dfrac{1}{{{v_1}}} - \dfrac{1}{u} = \dfrac{1}{{{f_1}}}\\_\\_\\_\\_\\_\\_\\_\left( 1 \right)
Similarly, for the image formed by lens B, we get
\dfrac{1}{v} - \dfrac{1}{{{v_1}}} = \dfrac{1}{{{f_2}}}\\_\\_\\_\\_\\_\\_\\_\left( 2 \right)
On adding $($1 ) and $($2 ), we get
$\dfrac{1}{v} - \dfrac{1}{u} = \dfrac{1}{{{f_1}}} + \dfrac{1}{{{f_2}}}$
If the two lenses are considered as equal to a single lens of focal length f, we get
$\dfrac{1}{v} - \dfrac{1}{u} = \dfrac{1}{f}$
$\Rightarrow \dfrac{1}{f} = \dfrac{1}{{{f_1}}} + \dfrac{1}{{{f_2}}}$
$\Rightarrow \dfrac{1}{f} = \dfrac{{{f_2} + {f_1}}}{{{f_1}{f_2}}}$
$\Rightarrow f = \dfrac{{{f_1}{f_2}}}{{{f_1} + {f_2}}}$

The expression is $f = \dfrac{{{f_1}{f_2}}}{{{f_1} + {f_2}}}$.

Note: 1) The focal length of the mirror is the distance between the pole and the focus of the mirror.
2) Focal length of the mirror is a measure of the power of the mirror.
3) Thin lenses have the same focal length on either side.