Question

Derive an expression for acceleration due to gravity at depth ‘h’ below earth’s surface.

Answer 1

In order to derive the expression for acceleration due to gravity, we need to use the formula of Newton’s law of universal gravitation and Newton's second law of motion. Newton's second law states that an object is accelerated whenever a net external force acts on it and that force is equal to product of mass and acceleration while Newton law of gravitation states that every object exerts a gravitational force on the other object

Complete step-by-step answer:
Let M be the mass of the earth
R be the radius of the earth
${g_h}$ be the acceleration at depth h from the surface and g be the gravitational acceleration on the surface.
$\rho$ be the density of the earth.

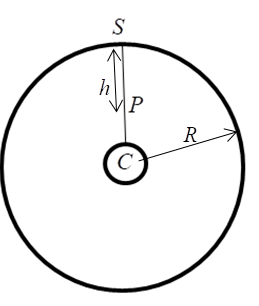
Assume that earth is a circle of radius R and has a uniform density.
From the figure P is the point inside the earth at depth ‘h’ from the surface
Therefore

{CS - CP = h} \\\ {CP = CS - h} \\\ {\therefore CS = R} \\\ {CP{\text{ = }}R - h...................\left( 1 \right)} \end{array}$$ As we know the acceleration due to gravity is given as $g = \dfrac{{GM}}{{{R^2}}}$ Mass of the earth in terms of density and volume can be written as $M = \dfrac{4}{3}\pi {R^3}\rho $ Substituting this value of mass in the equation of acceleration due to gravity $g = \dfrac{{4G\pi R\rho }}{3}..................\left( 2 \right)$ The acceleration due to gravity at depth h is given by $ {g_h} = \dfrac{{G \times {\text{mass of the sphere with radius CP}}}}{{C{P^2}}} \\\ {g_h} = \dfrac{{G \times \dfrac{{4\pi C{P^3}\rho }}{3}}}{{C{P^2}}} \\\ {g_h} = \dfrac{{4G\pi CP\rho }}{3}..........\left( 3 \right) \\\ $ Now dividing equation (3) by equation (2), we get $ \dfrac{{{g_h}}}{g} = \dfrac{{\dfrac{{4G\pi CP\rho }}{3}}}{{\dfrac{{4G\pi R\rho }}{3}}} \\\ \dfrac{{{g_h}}}{g} = \dfrac{{CP}}{R} = \dfrac{{R - h}}{R}\,\,\,\,\,\,\left[ {{\text{using equation }}\left( 1 \right)} \right] \\\ {g_h} = g\left( {1 - \dfrac{h}{R}} \right) \\\ $ Therefore, the acceleration due to gravity decreases linearly with depth and it becomes zero at the center of the earth. **Note:** As we know that earth exerts a force on us known as gravitational force due to which whenever anything goes above or below the surface of the earth it experiences this force of attraction towards the centre of earth. And due to which there is an acceleration called acceleration due to gravity whose value is $9.8m/{s^2}$. But this value varies with the variation of our positions below the earth surface or above it.