Question
Question: Derivative of $log_2(logx)$ with respect to $x$ is...
Derivative of log2(logx) with respect to x is
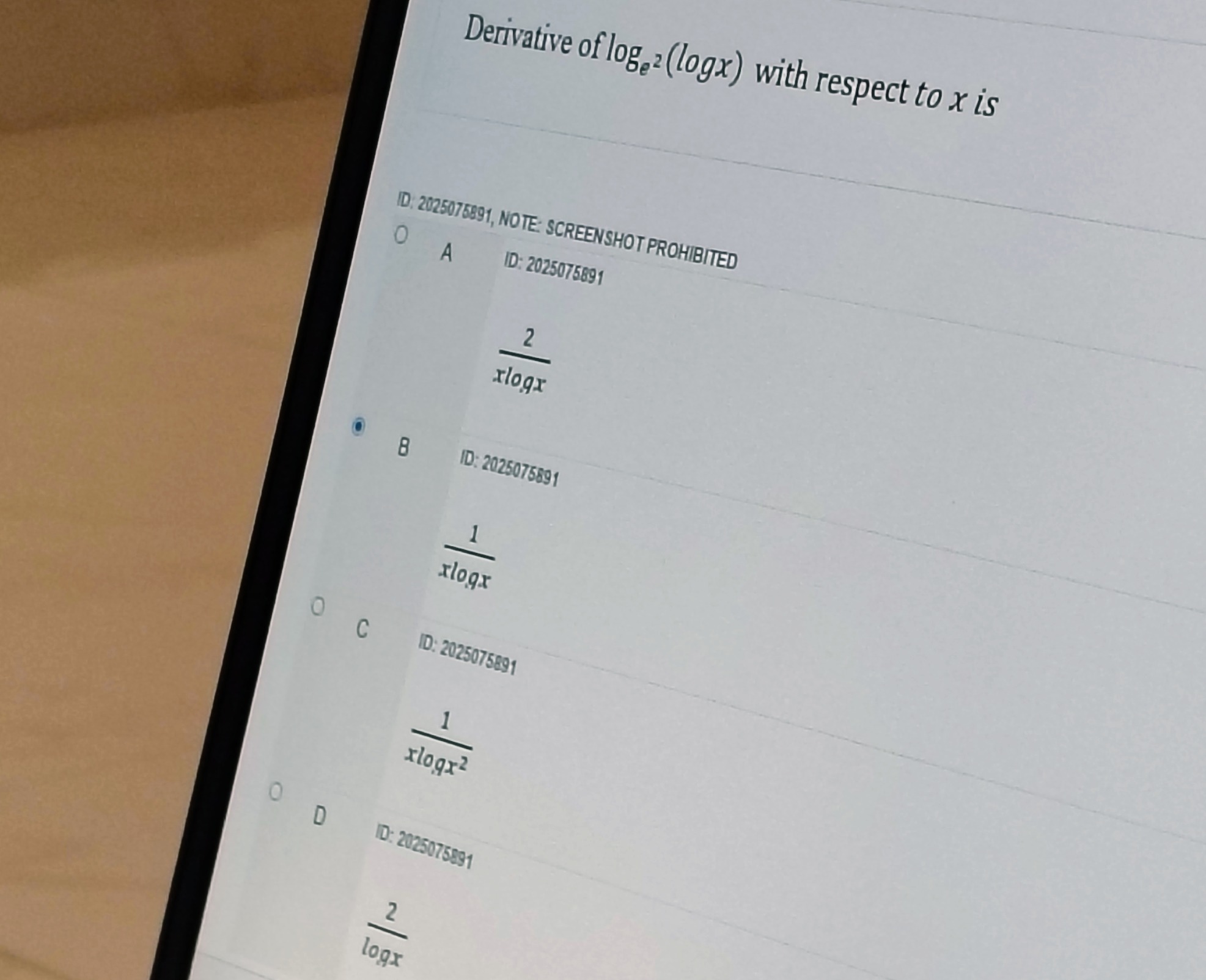
xlogx2
xlogx1
xlogx21
logx2
xlogx1
Solution
To find the derivative of log2(logx) with respect to x, we use the chain rule and the change of base formula for logarithms.
Let the given function be y=log2(logx).
First, recall the formula for the derivative of a logarithm with an arbitrary base: dud(logbu)=u⋅lnb1
In our case, the outer function is log2(u), where u=logx. So, applying the chain rule, we have: dxdy=dud(log2u)⋅dxdu dxdy=u⋅ln21⋅dxd(logx) Substitute u=logx: dxdy=logx⋅ln21⋅dxd(logx)
Now, we need to determine the base of the inner logarithm, logx. In calculus, when the base of logx is not explicitly specified, it is conventionally understood to be the natural logarithm (base e), i.e., logx=lnx.
Assuming logx=lnx: The derivative of lnx is dxd(lnx)=x1.
Substitute this into our expression for dxdy: dxdy=lnx⋅ln21⋅x1 dxdy=x⋅lnx⋅ln21
Now, let's compare this result with the given options. The options are: A: xlogx2 B: xlogx1 C: xlogx21 D: logx2
None of the options contain ln2 in the denominator. This suggests a potential common convention or a typo in the question. In many competitive exams, if logx is written without a base, it's often interpreted as lnx. If a question involving logb(logx) results in options without lnb, it often implies that the outermost logarithm was also intended to be base e.
Let's consider the possibility that the question implicitly intended to ask for the derivative of ln(logx), where logx means lnx. If the function was y=ln(lnx): dxdy=lnx1⋅dxd(lnx) (by chain rule) dxdy=lnx1⋅x1 dxdy=x⋅lnx1
If we assume that logx in the options also refers to lnx, then x⋅lnx1 is equivalent to x⋅logx1. This matches option B.
Given that this is a multiple-choice question and option B is a direct match under the assumption that the outermost logarithm was ln instead of log2, this is the most probable intended answer. The explicit log2 might be a distractor or a mistake in the question phrasing, as the ln2 factor is missing from all options.
