Question

$\Delta ABC$ has vertices (0,0), (11,60) and (91,0). If the line y=kx cuts the triangle into two triangles of equal area, then k is equal to
${\text{A}}{\text{. }}\dfrac{{30}}{{51}} \\\ {\text{B}}{\text{. }}\dfrac{4}{7} \\\ {\text{C}}{\text{. }}\dfrac{7}{4} \\\ {\text{D}}{\text{. }}\dfrac{{30}}{{91}} \\\$

Answer 1

Hint: In this question first we need to calculate the area of triangle ABC . Then, we have to draw a line y=kx which intersects BC at point D. And the area of triangle ADC is half of the area of triangle ABC. Now, find the area in terms of “kx” and equate it to numerical value and find the value of x in terms of “k”. And then equate the slope of line BC and CD to get the value of “k”.

Complete step-by-step answer:

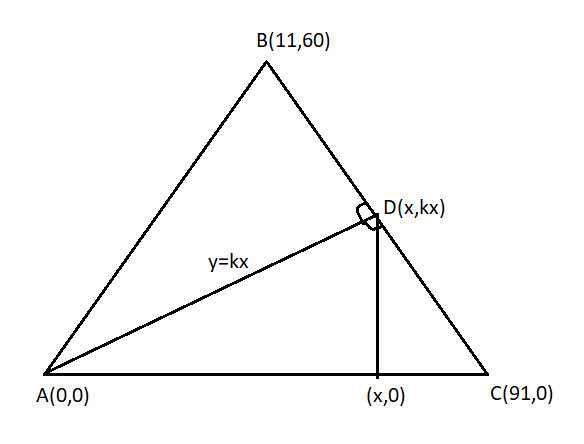
We have , triangle ABC
Coordinates of triangle are
A=(0,0)
B=(11,60)
C=(91,0)
First we have to calculate the area of triangle ABC, for this we require height(h) so draw a perpendicular from vertex B to base(B) which is AC.
Then, the height (h) of triangle ABC is 60 and Base(B) is 91.
Now, area of triangle ABC=$\dfrac{1}{2} \times {\text{Base}} \times {\text{Height}}$
=$\dfrac{1}{2} \times 91 \times 60$
= 2730 sq.unit ---- eq.1
Now, draw line y = kx which cuts the triangle ABC in two equal areas and cut BC at point D whose coordinate is (x,kx)
Now, we know by drawing y=kx the area of triangle ADC which is half of the area of triangle ABC.
Then, area of triangle ADC= $\dfrac{1}{2}({\text{Area of triangle ABC)}}$
=$\dfrac{1}{2}(2730)$
=$1365$sq. unit -----eq.2
Now, we have to find the area of triangle ADC in terms of “k” . For this we have to draw perpendicular from point “D” to base AC. Then the height (h) of triangle ADC is kx and the base of it is 91.
Then, the area of triangle ADC = $\dfrac{1}{2} \times kx \times 91$ ----eq.3
On equating eq.2 and eq.3 we get
$\Rightarrow \dfrac{1}{2} \times kx \times 91 = 1365 \\\ \Rightarrow kx = 30{\text{ ------ -----eq}}{\text{.4}} \\\$
And,
$\Rightarrow x = \dfrac{{30}}{k}{\text{ ----------eq}}{\text{.5}}$
Now, the coordinates of point D= $\left( {\dfrac{{30}}{k},30} \right){\text{ }}$
We know the line BC has two parts BD and CD.
Then,
Slope of BD= slope of CD
We know, the slope of a line passing through two given points let say X(p,q) and Y(h,k)
Then, slope of line =$\dfrac{{k - q}}{{h - p}}$
Now, the slope of line BD is
Where B(11,60) and D$\left( {\dfrac{{30}}{k},30} \right){\text{ }}$
Then, slope of BD =
$\Rightarrow \dfrac{{60 - 30}}{{11 - \dfrac{{30}}{k}}}{\text{ }} \\\ \Rightarrow \dfrac{{60 - 30}}{{11 - \dfrac{{30}}{k}}}{\text{ -------- eq}}{\text{.6}} \\\$
Similarly, the slope of CD =$\dfrac{{30}}{{\dfrac{{30}}{k} - 91}}{\text{ ---------eq}}{\text{.7}}$
On equating eq.6 with eq.7, we get
$\Rightarrow \dfrac{{30}}{{11 - \dfrac{{30}}{k}}} = \dfrac{{30}}{{\dfrac{{30}}{k} - 91}}$
On solving above equation, we get
$\Rightarrow \dfrac{{30}}{k} - 91 = 11 - \dfrac{{30}}{k} \\\ \Rightarrow \dfrac{{60}}{k} = 102 \\\ \Rightarrow k = \dfrac{{60}}{{102}} \\\ \Rightarrow k = \dfrac{{30}}{{51}} \\\$
Hence, option A. is correct.

Note:-Whenever you get this type of question the key concept to solve is to learn the formula of area of triangle which is given by $\dfrac{1}{2} \times {\text{Base}} \times {\text{Height}}$ and the slope of a line passing through two given points let say X(p,q) and Y(h,k) is given by $\dfrac{{k - q}}{{h - p}}$.