Question

Define the term self-inductance of a solenoid. Obtain the expression for the magnetic energy stored in an inductor of self-inductance $L$ to build up a current through it.

Answer 1

Hint: When current is passed through a solenoid, it develops some flux associated with the solenoid; we can find that flux with the help of magnetic field inside the solenoid. For calculating magnetic energy, we will use the formula of total work done by the current in the solenoid.

Formula used:
$L=\dfrac{\phi }{I}={{\mu }_{o}}{{N}^{2}}\pi {{r}^{2}}l$
$U=\dfrac{1}{2}L{{I}^{2}}$

Complete step by step answer:
Self-inductance of a solenoid is defined as the flux associated with the solenoid when a unit amount of current is passed through it.
Let us consider a long solenoid of length $l$ and radius $r$, having $n$ turns per unit length of solenoid, and carrying a current $I$.

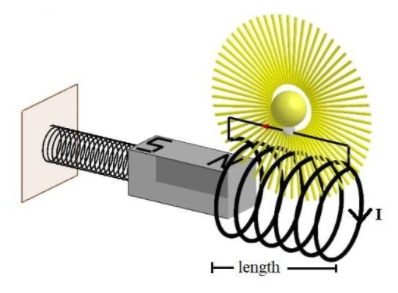
Since the amount of current through each loop is the same, the longitudinal magnetic field within the solenoid is approximately uniform. It is given by the formula,
$B={{\mu }_{o}}NI$
Total flux through the solenoid is,
$\phi =Nl{{\mu }_{o}}NI\pi {{r}^{2}}$
Therefore, self-inductance of solenoid is,
$L=\dfrac{\phi }{I}={{\mu }_{o}}{{N}^{2}}\pi {{r}^{2}}l$
Self-inductance of a solenoid only depends on the geometric quantities of solenoid, such as number of turns per unit length of solenoid and cross-sectional area of each turn.
For finding magnetic energy stored in the inductor, let’s consider the below circuit

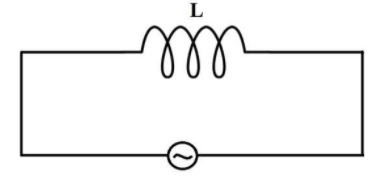
Emf in the circuit $e=-L\dfrac{dI}{dt}$
The direction of the induced emf is such that it opposes its very own cause which produces it, it means that it opposes the change of current through the coil.
For calculating the work done and magnetic energy stored in the solenoid, we will take the magnitude of emf induced.
$\left| e \right|=L\dfrac{dI}{dt}$
It gives, $dI=\dfrac{e}{L}dt$
Small amount of work done is given by,
$dW=eIdt$
Total work,

& W=\int{eIdt} \\\ & =\int\limits_{0}^{1}{LIdl}=\dfrac{1}{2}L{{I}^{2}} \end{aligned}$$ This work done will be stored as the magnetic energy in the solenoid $U=\dfrac{1}{2}L{{I}^{2}}$ Value of magnetic energy$=\dfrac{1}{2}L{{I}^{2}}$. Note: Students should note here that self-inductance of a solenoid is a quantity which only depends on the length of solenoid, number of turns per unit length of solenoid and the cross-sectional area of the turns in solenoid. For increasing self-inductance of a solenoid, we can either increase the number of turns in solenoid or by increasing the diameter of the turns in solenoid.