Question
Question: Define the current sensitivity of a galvanometer. Write S.I unit Figure shows two circuits each ha...
Define the current sensitivity of a galvanometer. Write S.I unit
Figure shows two circuits each having a galvanometer and a battery of 3V. When the galvanometer in each arrangement do not show any deflection obtain the ratio R2R1
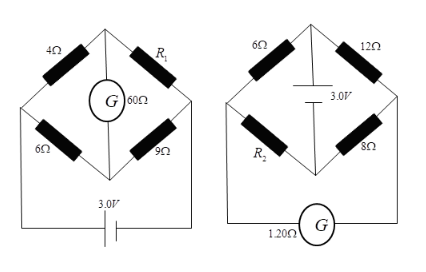
Solution
Hint- In order to solve this question, we will use the concept of wheatstone bridge. In a wheatstone bridge, the bridge is said to be balanced when the galvanometer shows zero deflection. We will use the condition of zero deflection of the galvanometer to find the unknown value of the resistance and then proceed accordingly.
Complete step-by-step answer:
Condition for balanced bridge-
R3R1=R4R2
Current sensitivity- The term current sensitivity is defined as when current flow through the galvanometer coil, the coil shows deflection.
Mathematically it can be represented as
Is=Tθ=cnBA
Where n is the number of turns in the coil, B is the magnetic field around the coil, A is the cross sectional area of the coil and c is the restoring torque.
The SI unit of the current sensitivity is radian per ampere.
Now for calculating the value of unknown resistance we will use the condition of balanced bridge.
First for the value of resistance R1
R3Rx=R4R2
Where Rx=4,R2=R1,R3=9,R4=6
Substituting these values in the above equation
9R1=64 R1=6Ω
Now for the value of resistance R2 from figure second
R3R1=RxR2
Where R1=6,R2=12,R3=8,Rx=R2
Substituting these values in the above equation
R26=812 R2=126×8=4Ω
Therefore the ratio of R2R1 is
R2R1=46=23
Note- In order to solve questions related to the wheatstone bridge, learn the basic concept behind the wheatstone bridge and also remember the wheatstone bridge is used to find the value of the unknown resistance. It is used to measure the value of the resistance very precisely. Other applications of the wheatstone bridge is ; it is used with operational amplifiers to measure temperature, light, strain etc.
