Question

Define refractive index. You are given kerosene, turpentine and water. In which of these does the light travel faster? Which of these liquids are optically denser? Find out the speed of light in turpentine if the light travels from air to the turpentine.
RI of water is 1.33, Kerosene 1.44, turpentine 1.47. Speed of light in air is $3 \times {10^8}m/s$ .

Answer 1

A material can reflect or refract the light. Reflection will happen if one side is reflecting and the other side is opaque. Refraction is the bending of light. If light travels from lighter to the denser medium it will bend and this is called refraction. Speed of light varies in different materials with refractive index.

Complete Step By Step Answer:
Refractive Index: It is the property of material or also known as the dimensionless number. Found out by taking the ratio of speed of light in air and the speed of light in material.
$RI\,of\,material = \dfrac{{speed\,of\,light\,in\,air}}{{speed\,of\,light\,in\,material}}$

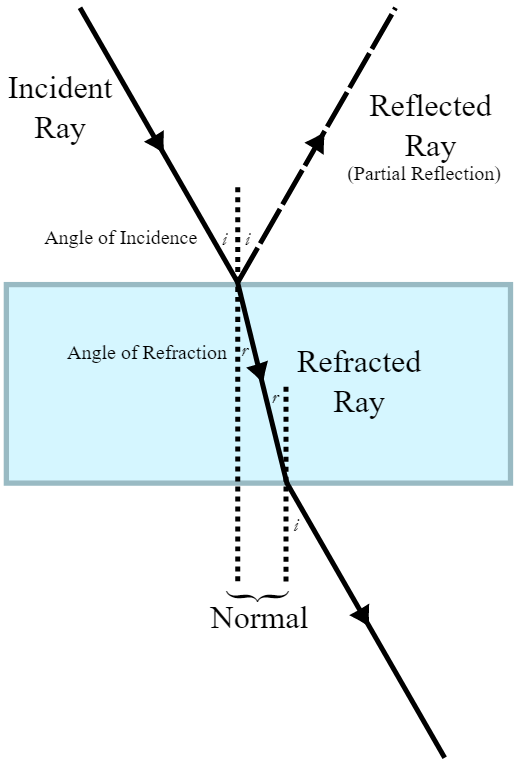
More will be the Refractive index the more the light bends in that particular medium. The speed of light is inversely proportional to the refractive index.
The optical density is the measure of refractive index or can be said that it is directly proportional to the refractive index. More the refractive index, the more will be the optical density of that material.
We are given the materials as water, kerosene and turpentine with RI values $1.33,{\text{ }}1.44,{\text{ }}1.47$.
As we can observe the RI of turpentine > kerosene > water.
The turpentine will be optically denser as compared to the other two.
In the final section of the section we are asked to find out the speed of light in turpentine.
We know from the formula that
$RI\,of\,material = \dfrac{{speed\,of\,light\,in\,air}}{{speed\,of\,light\,in\,material}}$
Given that Speed of light in air is $3 \times {10^8}m/s$ .
RI of turpentine is 1.47
Substituting the values in the equation we get,
$1.47 = \dfrac{{3 \times {{10}^8}}}{v}$
Here, v is the speed in the material turpentine.
Rearranging and solving the equation.
v = \dfrac{{3 \times {{10}^8}}}{{1.47}} \\\ \Rightarrow v = 2.04 \times {10^8}m/s \\\
Hence, the velocity in the turpentine is $\Rightarrow v = 2.04 \times {10^8}m/s$ .

Note :
From the law of refraction we have, “The ratio of the sine of the angle of incidence to the sine of the angle of refraction will always remain constant. It is equal to the refractive index of the medium. It is known as the Snell’s Law.”
The incident ray and refracted ray lies on the opposite sides of the normal at the point of incidence.
The incident, refracted and the normal at the point of incidence lie in the same plane.