Question

Define refractive index of a transparent medium. For a ray of light that passes through a triangular prism, plot a graph showing the variation of the angle of deviation with the angle of incidence.

Answer 1

Firstly, you could recall the definition of the refractive index. Then you could think of the trend shown by the angle of deviation with varying angle of incidence. By understanding this variation of angle of deviation with angle incidence, you could plot a graph on the same. You could also mark the angle of minimum deviation in the plot.

Complete answer:
In the question, we are asked to define the refractive index of a transparent medium and we are also asked to plot a graph for a ray of light passing through a triangular prism showing the variation of angle of deviation with the angle of incidence.
Refractive index is basically a dimensionless number which can be defined as the ratio of velocity of light in vacuum or air to the velocity of light in a medium. That is,
$n=\dfrac{c}{v}$
Where, n is the refractive index of the medium with velocity of light v and c is the velocity of light in vacuum.
We could also define a refractive index as the factor by which the wavelength and speed of the light is reduced with respect to their value observed in vacuum.
For a triangular prism:

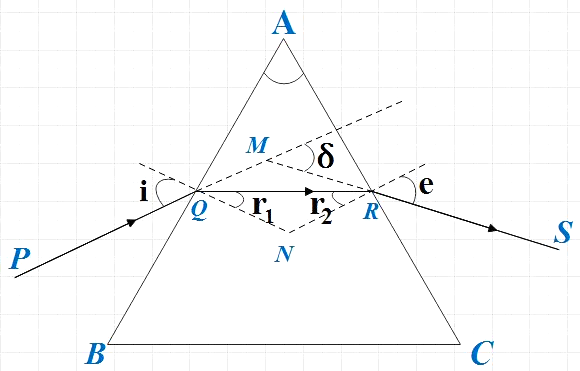
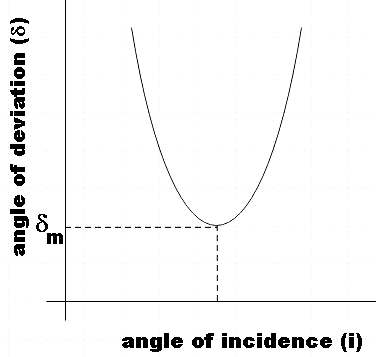
The variation of angle of deviation with incident angle is observed as follows: if we were to increase the angle of incidence, the angle of deviation $\delta$decreases initially and then reaches a minimum value. On increasing the angle of incidence further, the angle of deviation also increases with it.
If we were to plot a graph showing the variation of the angle of deviation with the angle of incidence, it would be as shown below,

Note:
If n is the refractive index of the medium, D is the angle of minimum deviation and A is the angle of prism then,
$n=\dfrac{\sin \left( \dfrac{A+D}{2} \right)}{\sin \left( \dfrac{A}{2} \right)}$
The refractive index is also known to vary with wavelength and this further results in dispersion of light into its constituent colors.